2024. 3. 17. 17:41ㆍ딥러닝 모델: 파이토치
깊은 인공신경망을 학습하다보면 역전파 과정에서 입력층으로 갈수록 기울기가 점차적으로 작아지는 현상이 발생할 수 있다. 입력층에 가까운 층들에서 가중치들이 제대로 업데이트 되지 않으면 최적의 모델을 찾을 수 없다. 이를 기울기 소실(Gradient Vanishing)이라고 한다.
반대의 경우로, 기울기가 점차 커지면서 가중치들이 비정상적으로 큰 값이 되어 발산되기도 한다. 이를 기울기 폭주(Gradient Exploding)이라고 하며, 뒤에서 배울 순환신경망(Recurrent Neural Network, RNN)에서 발생할 수 있다.
여기서는 기울기 소실 또는 기울기 폭주를 막는 방법들에 대해 다룬다.
♣ ReLU와 ReLU의 변형들
시그모이드 함수를 사용하면 입력의 절대값이 클 경우, 시그모이드 함수의 출력값이 0 또는 1에 수렴하면서 기울기가 0에 가까워진다. 그래서 역전파 과정에서 전파할 기울기가 점차 사라져서 입력층 방향으로 갈수록 제대로 역전파가 되지 않는 기울기 소실 문제가 발생할 수 있다.
기울기 소실을 완화하는 가장 간단한 방법은 은닉층의 활성화 함수로 시그모이드나 하이퍼볼릭탄젠트 함수 대신에 ReLU나 ReLU의 변형 함수와 같은 Leaky ReLU를 사용하는 것이다.
- 은닉층에서는 시그모이드 함수 사용하지 않기
- Leaky ReLU를 사용하면 모든 입력값에 대해서 기울기가 0에 수렴하지 않기 때문에 죽은 ReLU 문제를 해결한다.
- 은닉층에서는 ReLU나 Leaky ReLU와 같은 ReLU 함수의 변형들을 사용한다.
♣ 가중치 초기화(Weight initialization)
같은 모델을 훈련시키더라도 가중치가 초기에 어떤 값을 가졌느냐에 따라서 모델의 훈련 결과가 달라지기도 한다. 어느 지점에서 weight가 초기화되었느냐에 따라 Local minimum에 빠질 수도 있고, Global minimum에 도달할 수도 있다.
즉 가중치 초기화만 적절히 해도 기울기 소실 문제를 완화시킬 수 있다. 활성함수의 출력값의 분산이 layer를 거듭하더라도 일정하게 유지되는 것이 좋다.

- 모든 weight들이 0으로 초기화되면 layer를 지나더라도 weight의 값이 변하지 않는다. 당연히 각 weight에 대한 gradient값도 0이 되므로 모델이 데이터를 학습하지 못한다.
- 모든 weight들이 동일한 값으로 초기화되면 이는 뉴런이 하나만 있는 신경망과 다를 바 없어진다. (symmetry problem)
- 모든 weight들이 매우 작은 값으로 초기화되면 손실 함수를 줄이는 데 시간이 많이 걸리기는 하지만 유의미한 효과가 나타난다. 각 weight에 대한 graidient값도 시간이 충분히 지나면서 점점 작아진다.
- 모든 weight들이 적합한 값으로 초기화되면 손실 함수가 빠르게 줄어든다. 또한 decision boundary 역시 빠르게 좁힐 수 있다.
- 모든 weight들이 매우 큰 값으로 초기화되면 학습과정이 무척 불안정하다. 또한 decision boundary를 빠르게 학습한다.
Random Initialization
1. 세이비어 초기화(Xavier Initialization/ Glorot Initialization)
이 방법은 균등 분포(Uniform Distribution)로 초기화 하는 경우 또는 정규 분포(Normal distribution)로 초기화하는 경우 두 가지로 나뉘며, 이전 층의 뉴런 개수와 다음 층의 뉴런 개수를 가지고 식을 세운다. 이전 층의 뉴런의 개수를 n in, 다음 층의 뉴런의 개수를 n out이라고 해보자.
균등 분포를 사용하여 가중치를 초기화할 경우, 다음과 같은 균등 분포 범위를 사용한다.
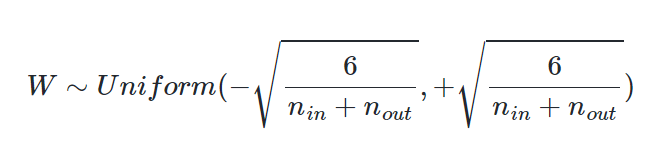
정규 분포로 초기화할 경우에는 평균이 0이고 표준편차가 다음을 만족하도록 한다.

세이비어 초기화는 여러 층이 기울기 분산 사이에서 균형을 맞춰서 특정 층이 너무 주목을 받거나 다른 층이 뒤쳐지는 것을 막는다. 즉 출력함수의 출력값의 분산이 대략적으로 유지되도록 한다. 그런데 세이비어 초기화는 시그모이드 함수나 하이퍼볼릭 탄젠트 함수와 같은 S자 형태인 활성화 함수와 함께 사용할 경우에는 좋은 성능을 보이지만, ReLU와 함께 사용할 경우에는 성능이 좋지 않다. ReLU 함수 또는 ReLU의 변형 함수들을 활성화 함수로 사용할 경우에는 다른 초기화 방법을 사용하는 것이 좋은데, 이를 He 초기화(He initialization)라고 한다.
2. He 초기화(He initialization)
He 초기화는 세이비어 초기화와 유사하게 정규 분포와 균등 분포 두 가지 경우로 나뉜다. 다만 He 초기화는 세이비어 초기화와 다르게 다음 층의 뉴런의 수를 반영하지 않는다. 전과 같이 이전 층의 뉴런 개수를 n in 이라고 하자.
He 초기화는 균등 분포로 초기화할 경우, 다음과 같은 균등 분포 범위를 가지도록 한다.

정규 분포로 초기화할 경우에는 표준편차가 다음을 만족하도록 한다.

- 시그모이드 함수, 하이퍼볼릭탄젠트 함수를 사용할 경우에는 세이비어 초기화 방법이 효율적이다.
- ReLU 계 함수를 사용할 경우에는 He 초기화 방법이 효율적이다.
- ReLU + He 초기화 방법이 좀 더 보편적이다.
3. Random normal initialization
가중치를 0 주변으로 초기화한다. 이는 가중치가 saturated region에서 초기화되는 것을 막기 위함이다.

Initialization from Transfer Learning
1. ImageNet pre-trained (for Comupter Vision model)
ImageNet은 1000개의 class와 1400만 장의 image data로 구성된다.
2. Masked Langguage Modeling(MLM) pre-trained (for NLP model)
MLM = 문장의 일부를 가리고 가려진 단어들에 대해서 맞추도록 모델을 학습시키는 task
♣ 배치 정규화(Batch Normalization)
ReLU 계열의 함수와 he 초기화를 사용하는 것만으로도 어느 정도 기울기 소실과 폭주를 완화할 수 있지만, 이 두 방법을 사용하더라도 훈련 중 언제든 기울기 소실과 폭주가 다시 발생할 수 있다. 기울기 소실이나 폭주를 예방하는 또 다른 방법에는 배치 정규화가 있다. 배치 정규화는 인공신경망의 각 층에 들어가는 입력을 평균과 분산으로 정규화하여 학습을 효율적으로 만든다.
1. 내부 공변량 변화(Internal Covariate Shift)
내부 공변량 변화란 학습 과정에서 층 별로 입력 데이터 분포가 달라지는 현상을 의미한다. 이전 층들의 학습에 의해 이전 층의 가중치 값이 바뀌게 되면, 현재 층에 전달되는 입력 데이터의 분포가 현재 층이 학습했던 시점의 분포와 차이가 발생한다.
- 공변량 변화는 훈련 데이터의 분포와 테스트 데이터의 분포가 다른 경우를 의미한다.
- 내부 공변량 변화는 신경망 층 사이에서 발생하는 입력 데이터의 분포 변화를 의미한다.
2. 배치 정규화
배치 정규화는 한 번에 들어오는 배치 단위로 정규화하는 것을 의미한다. 배치 정규화는 각 층에서 활성화 함수를 통과하기 전에 수행된다. 배치 정규화를 요약하면 다음과 같다.
입력에 대한 평균을 0으로 만들고 정규화를 한다. 그리고 정규화된 데이터에 대해서 스케일과 시프트를 수행한다. 이때 두 개의 매개변수 람다와 베타를 사용하는데, 람다는 스케일을 위해 사용하고 베타는 시프트를 하는 것에 사용하며 다음 레이어에 일정한 범위의 값들만 전달되게 한다.
배치 정규화의 수식은 다음과 같다(BN은 배치 정규화를 의미함)
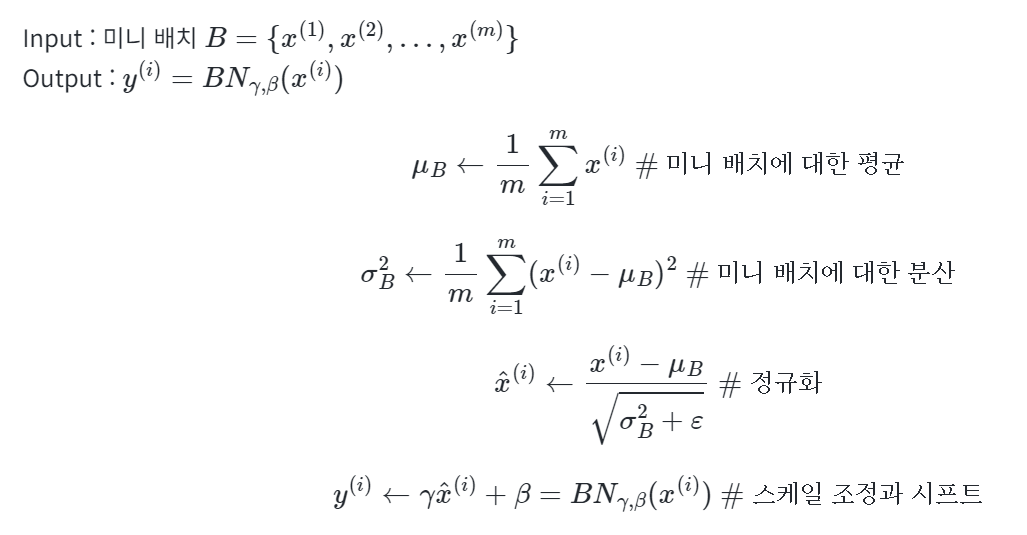

배치 정규화는 학습 시 배치 단위의 평균과 분산들을 차례대로 받아서 이동 평균과 이동 분산을 저장해놓았다가 테스트할 때는 해당 배치의 평균과 분산을 구하지 않고 구해놓았던 평균과 분산으로 정규화를 한다.
- 배치 정규화를 사용하면 시그모이드 함수나 하이퍼볼릭탄젠트 함수를 사용해도 기울기 소실 문제가 크게 개선된다.
- 가중치 초기화에 훨씬 덜 민감해진다.
- 훨씬 큰 학습률을 사용할 수 있어 학습 속도를 개선시킨다.
- 미니 배치마다 평균과 표준편차를 계산하므로 훈련 데이터에 일종의 잡음을 넣는 부수 효과로 과적합을 방지하는 효과도 낸다. 하지만 부수적 효과이므로 드롭 아웃과 함께 사용하는 것이 좋다.
- 배치 정규화는 모델을 복잡하게 하며, 추가 계산을 하는 것이므로 테스트 데이터에 대한 예측 시에 실행 시간이 느려진다. 그래서 서비스 속도를 고려하는 관점에서는 배치 정규화가 꼭 필요한지 고민이 필요하다.
- 배치 정규화의 효과는 굉장하지만 내부 공변량 변화 때문은 아니라는 논문도 존재한다.
3. 배치 정규화의 한계
- 미니 배치 크기에 의존적이다.
배치 정규화는 너무 작은 배치 크기에서는 잘 동작하지 않을 수 있다. 작은 미니 배치에서는 배치 정규화의 효과가 극단적으로 작용되어 훈련에 악영향을 줄 수 있다. 배치 정규화를 적용할 때는 작은 미니 배치보다는 크기가 어느 정도 되는 미니 배치에서 실시하는 것이 좋다.
- RNN에 적용하기 어렵다.
RNN은 각 시점(time step)마다 다른 통계치를 가진다. 이는 RNN에 배치 정규화를 적용하는 것을 어렵게 한다.
다음으로는 배치 크기에 의존적이지 않으며, RNN에도 적용하는 것이 수월한 층 정규화라는 방법을 소개한다.
♣ 층 정규화(layer Normalization)
층 정규화를 이해하기에 앞서 배치 정규화를 시각화해보자. 다음은 m이 3이고, 특성(feature)의 수가 4일 때의 배치 정규화를 보여준다. 미니 배치란 동일한 특성(feature) 개수들을 가진 다수의 샘플임을 상기하자.

배치 정규화는 채널 수(특징 수) 만큼의 평균과 분산을 계산해야 한다.
층 정규화는 데이터별로 정규화한다.
♣ 참고 자료
Weight Initialization
https://ysg2997.tistory.com/14
[PyTorch] Weight Initialization (기울기 초기화)
딥러닝 모델 학습시 가중치를 초기화하고, 예측값과 실제 값의 차이를 loss function을 통해 구한다. 이후 loss를 줄이는 방향으로 가중치를 업데이트를 하게 된다. 결국 모델이 학습하는 대상은 optim
ysg2997.tistory.com
'딥러닝 모델: 파이토치' 카테고리의 다른 글
| Pytorch로 시작하는 딥러닝 입문(07-01. 순환 신경망, 파이토치의 nn.RNN()) (0) | 2024.03.18 |
|---|---|
| Pytorch로 시작하는 딥러닝 입문(07-01. 순환 신경망, Recurrent Neural Network, RNN) (0) | 2024.03.17 |
| Pytorch로 시작하는 딥러닝 입문(06-09. 과적합을 막은 방법들/augmentation, regularization, Dropout, Early stopping) (0) | 2024.03.16 |
| Pytorch로 시작하는 딥러닝 입문(06-08. 다층 퍼셉트론으로 MNIST 분류하기) (0) | 2024.03.16 |
| Pytorch로 시작하는 딥러닝 입문(06-07. 다층 퍼셉트론으로 손글씨 분류하기) (0) | 2024.03.14 |