2024. 5. 5. 10:41ㆍ알고리즘
♣ 휴리스틱
불충분한 시간이나 정보로 인하여 합리적인 판단을 할 수 없거나, 체계적이면서 합리적인 판단이 굳이 필요하지 않은 상황에서 사람들이 빠르게 사용할 수 있게 보다 용이하게 구성된 간편 추론의 방법을 의미한다.
휴리스틱은 기본적으로 최적해가 될 가능성이 없는 답들을 탐색하는 것을 방지하여 만들어 봐야 할 답의 수를 줄이는 것을 목표로 한다.
휴리스틱 관련 기법
- 가지치기(pruning) 기법
- Simulated Annealing (담금질 기법)
- Genetic Algorithms (유전 알고리즘)
♣ 그리디 알고리즘 vs 휴리스틱
그리디 알고리즘은 stage를 분할해 각 스테이지별로 최적해를 찾는다. 하지만 마지막 결과가 최적해임을 보장하지는 못하기 때문에 결과가 최적해인지 검증하는 단계가 필요하다. 마찬가지로 휴리스틱도 최적해를 보장하지 않을 수 있지만, 최적해와 근접한 결과값을 단시간에 제공해준다.
그리디 알고리즘은 시간 복잡도와 공간 복잡도가 상당히 높을 수 있지만, 휴리스틱은 시간을 절약할 수 있다.
♣ 알고리즘 vs 휴리스틱
알고리즘은 문제에 대한 자동화된 솔루션에 대한 설명이다 . 알고리즘이 수행하는 작업은 정확하게 정의되어 있으며 처음부터 어떤 결과를 얻게 될지 알 수 있다. (항상 최적해를 찾아내는 것은 아님)
일부 문제는 어려워서 적절한 시간 내에 적절한 해결책을 얻지 못할 수도 있는데, 이러한 경우에는 임의의 선택(학습된 추측)을 적용하여 훨씬 더 빨리 나쁘지 않은 솔루션을 얻을 수 있다. 이것이 바로 휴리스틱이다.
휴리스틱은 일종의 알고리즘이지만 문제의 가능한 모든 상태를 탐색하지 않거나 가장 가능성이 높은 상태를 탐색하는 것부터 시작한다. 어떤 경우에는 최상의 솔루션을 찾는 것이 아니라 일부 제약 조건에 맞는 솔루션을 찾는다. 좋은 휴리스틱은 짧은 시간에 해결책을 찾는 데 도움이 되지만 시도하지 않기로 선택한 상태에 유일한 해결책이 있는 경우에는 해결책을 찾지 못할 수도 있다.

♣ 백준 알고리즘 10819번(휴리스틱)
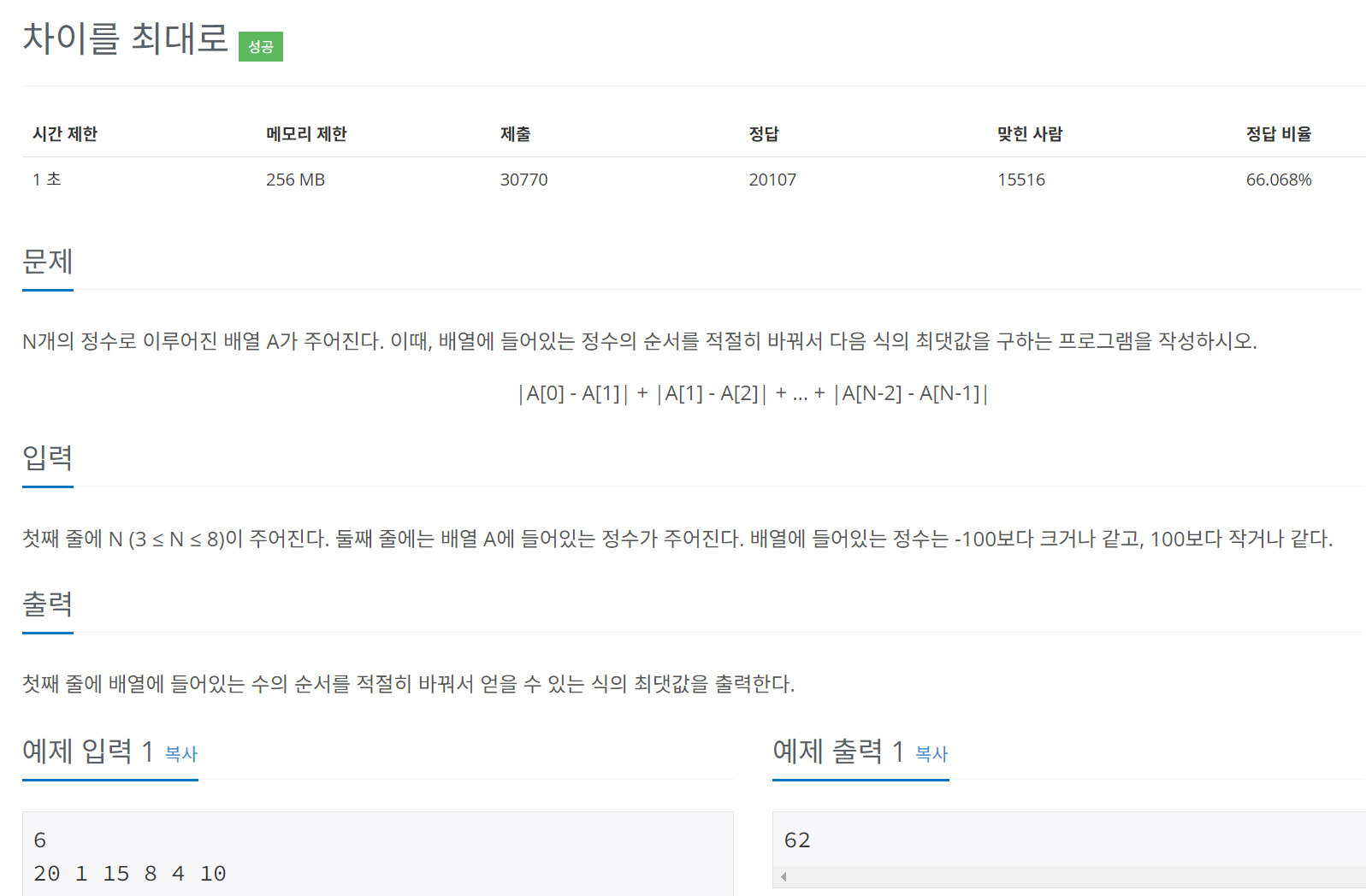
위의 문제는 n개의 수가 주어졌을 때 수의 순서를 적절히 바꾸어서 두 수의 차의 절대값이 가장 커지도록 하는 문제이다.
예를 들어 n = 6, 숫자는 20, 1, 15, 8, 4, 10일 때 절대값의 가장 큰 값을 구하려면 숫자를 아래와 같이 배열해야 한다.
8 20 4 15 1 10
abs(8-20) + abs(20-4) + abs(4-15) + abs(15-1) + abs(1-10) => 12 + 16 + 11 + 14 + 9 = 62
이 예시의 답을 찾으면서 가장 큰 값을 구하기 위해서는 숫자를 정렬한 후 두 그룹으로 나누어서 각 그룹에서 큰 것부터 배치해야 한다고 생각했다.
예를 들어 위의 숫자를 오름차순으로 배치하고 => [1, 4, 8, 10, 15, 20]
이를 두 그룹으로 나누고 => [1, 4, 8] [10, 15, 20]
두 그룹에서 가장 큰 수들부터 배치하는 것이다. 다만 이때 작은 그룹에 있는 수부터 배치한다. => [8, 20, 4, 15, 1, 10]
이 방법이 모든 예시에 다 맞을 것이라고 생각해서 아래와 같이 코드를 작성하였다.

그런데 이렇게 제출했더니 95퍼센트에서 틀리고 말았다. 질문게시판을 뒤져서 반례를 찾을 수 있었다.
3
3 1 3
n이 3이고 주어진 수가 3, 1, 3일 때 내가 만든 코드를 적용하면 front = [1, 3] , rear = [3] 이다.
이를 다시 배치하면 [3, 3, 1] 이 되고, abs(3-3) + abs(3-1) = 2가 답으로 나온다.
하지만 최댓값은 [3, 1, 3] 으로 배치했을 때의 abs(3-1) + abs(1-3) = 4 이다.
이 반례를 해결하기 위해 코드를 아래와 같이 수정하였다.

중간에 if rear[0] == front[-1], 즉 두 그룹으로 나누었을 때 큰 그룹에서 가장 작은 수와 작은 그룹에서 가장 큰 수의 값이 같으면 작은 그룹에 있는 가장 큰 수를 큰 그룹의 맨 앞으로 끼워넣은 것이다. 그렇게 해서 원래 규칙대로 배치한 후, 큰 그룹(rear)에 마지막으로 남아있는 수를 새로운 수열의 맨 앞에 넣었다.
3
3 1 3 일 때
front = [1, 3] rear = [3]
front[-1] == rear[0] 이므로 front[-1]을 rear의 0번째 index로 추가하기 => front = [1], rear = [3, 3]
이전의 규칙처럼 두 그룹의 수에서 가장 큰 것부터 가져와서 배열하기 => new = [1, 3] , rear에는 3이 남아있다.
rear에 수가 남아있으면 이를 new의 0번째 index에 추가한다.
new = [3, 1, 3] 이렇게 하면 원하는대로 절대값의 합이 4가 된다.
그런데 이렇게 고쳐서 제출했더니 오히려 33% 정도에서 틀리고 말았다. 반례를 포함시키려고 코드를 고침으로써 오히려 일반적인 예시에서 틀리게 된 것 같다.
♣ 백준 알고리즘 10819번(부르트포스 알고리즘)

문제에 딱 맞는 방법을 찾는 것을 포기하고 일반적인 순열을 만드는 알고리즘을 이용해서 모든 수 배열을 구하고 차의 절댓값을 더해서 최댓값을 출력하였다.
문제를 풀 수 있는 뚜렷한 방향이 있다면 그에 맞게 특정한 코드를 만들어보는 게 좋겠지만, 여러 가지 예외 사항이 튀어나오게 된다면 어디에나 사용할 수 있는 일반적인 알고리즘을 활용하는 게 나을 수도 있다!
♣ 참고 자료
https://velog.io/@joy37/Heuristic-Algorithm%EC%9D%B4%EB%9E%80
Heuristic Algorithm이란?
이전 포스팅에서 React의 diffing algorithm에 대한 이야기를 하며 heuristics 알고리즘을 이용한다고 말한 적이 있다. 휴리스틱 알고리즘은 중요한 정보만 고려해서 최선의 값을 찾아내는 알고리즘이라
velog.io
What is the difference between a heuristic and an algorithm?
What is the difference between a heuristic and an algorithm?
stackoverflow.com
https://www.baeldung.com/cs/heuristic-vs-algorithm
'알고리즘' 카테고리의 다른 글
| 비트마스킹(백준 알고리즘 2961번) (0) | 2024.05.21 |
|---|---|
| 자료구조(백준 알고리즘 5430번) (0) | 2024.05.14 |
| 그리디 알고리즘(백준 알고리즘 1931번) (0) | 2024.04.17 |
| 투 포인터(백준 알고리즘 1644번) (0) | 2024.03.31 |
| 백트래킹(백준 알고리즘 1987) (0) | 2024.03.29 |