2024. 7. 11. 19:46ㆍ알고리즘
♣ CCW
세 점 A, B, C가 존재할 때, 특정 선분에 대하여 특정 점이 왼쪽에 있는지(시계 방향) 오른쪽에 있는지(반시계 방향)를 판별할 수 있는 알고리즘이다. 아래 그림을 예로 들어보자.
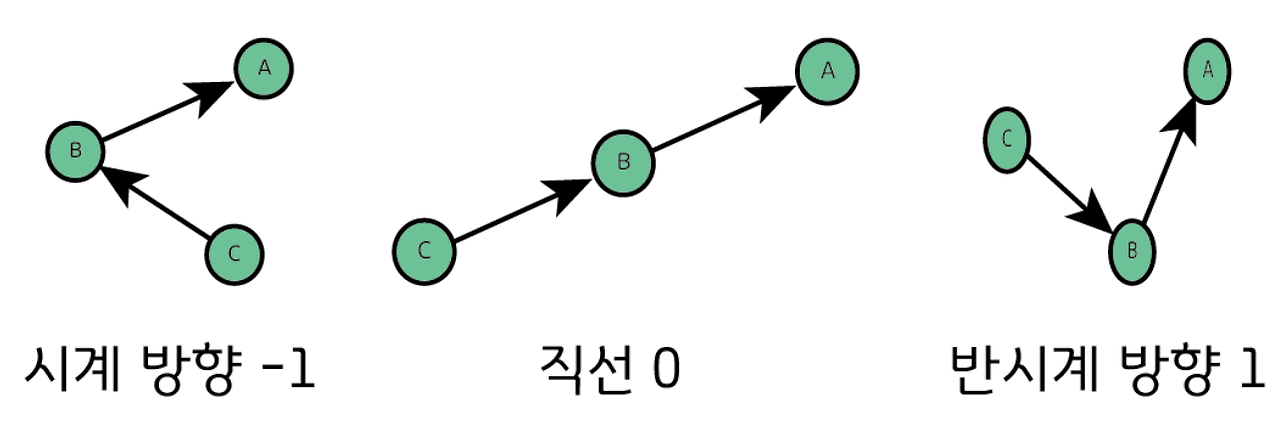
C -> B -> A로 진행하는데, 첫 번째 그림은 시계방향, 두 번째 그림은 직선, 세 번째 그림은 반시계 방향을 나타낸다.
즉 선분 CB에 대한 점 A의 위치라고 생각하면 점 A는 선분 CB에 대해 각 그림에 따라 시계방향, 직선, 반시계 방향에 위치하는 것이다.
CCW(Counter Clock Wise)는 이렇게 세 점을 이었을 때의 방향을 판단하는 데 유용하게 쓸 수 있는 알고리즘이다.
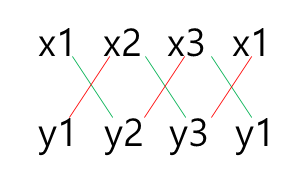
신발끈 공식
점 A, B, C를 보면 선분 CB에 대한 점 A의 위치(방향)을 구하는 것이므로 점 C를 (x1, y1), 점 B를 (x2, y2), 점 A를 (x3, y3)라고 한다. 위의 신발끈 공식을 사용하여
x1*y2 + x2*y3 + x3*y1 - x2*y1 - x3*y2 - x1*y3 를 계산한다. 이를 함수로 만들면 아래와 같다.
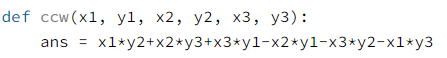
결과 ans이 0보다 크면 반시계 방향, 0이면 직선, 0보다 작으면 시계방향이다.
https://jy-deeplearning.tistory.com/100
CCW(Counter Clock Wise, 백준 알고리즘 11758번)
♣ CCW 세 점 A, B, C가 존재할 때, 특정 선분에 대하여 특정 점이 왼쪽에 있는지(시계 방향) 오른쪽에 있는지(반시계 방향)를 판별할 수 있는 알고리즘이다. 아래 그림을 예로 들어보자. C -> B -> A로
jy-deeplearning.tistory.com
♣ 백준 알고리즘 17386번(선분교차1)

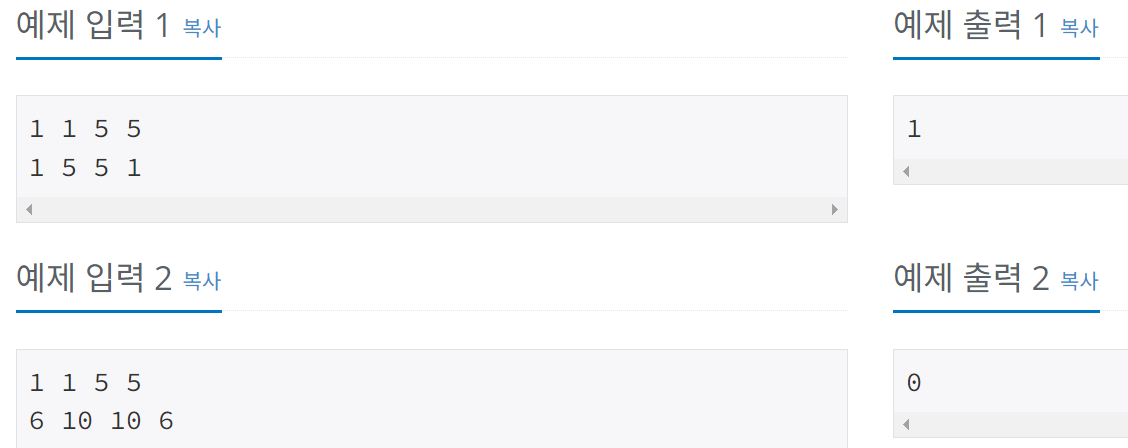
두 선분 L1, L2가 주어졌을 때 두 선분의 교차 여부를 알아보는 문제이다. 세 점이 일직선 위에 있는 경우는 없으므로, 두 선분이 만날 때는 아래 그림처럼 반드시 서로를 지나가야 한다.
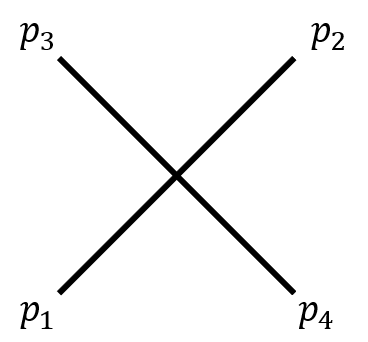
그림을 보면 선분 P1-P2를 기준으로 했을 때 P3는 시계 반대 방향, P4는 시계 방향에 있다. 즉 한 선분을 기준으로 해서 다른 선분의 두 점이 각각 다른 방향에 위치해야 한다. 즉 CCW를 사용하면 ans가 1, -1 두 가지가 나와야 한다.
두 개 선분이 만나지 않는 경우는 아래와 같다.
1) x1, y1 - x2, y2 에 대해 x3, y3 와 x4, y4가 모두 시계 방향에 있을 때

2) x1, y1 - x2, y2 에 대해 x3, y3 와 x4, y4가 모두 시계 반대 방향에 있을 때
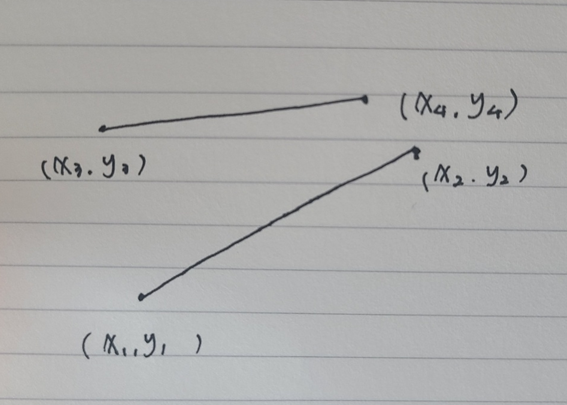
3) x3, y3 - x4, y4 에 대해 x1, y1과 x2, y2가 모두 시계 방향에 있을 때
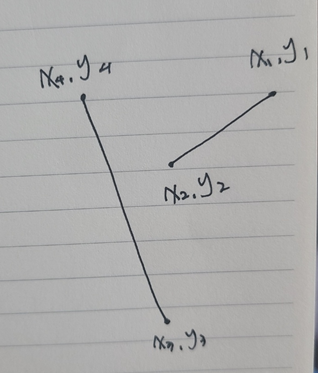
세 번째 예시를 찾느라 시간이 좀 걸렸다. 1, 2번과 다르게 x1, y1 - x2, y2에 대해서 x3, y3는 시계 방향에 있고 x4, y4는 시계반대방향에 있어서 ans가 -1, 1 임에도 불구하고 선분이 만나지 못하는 형태이다.
3) x3, y3 - x4, y4 에 대해 x1, y1과 x2, y2가 모두 시계 반대 방향에 있을 때
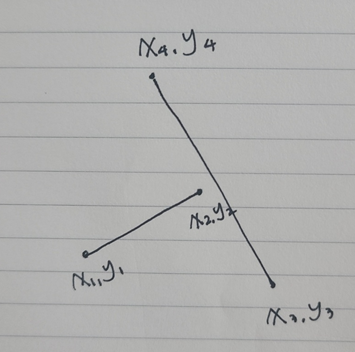
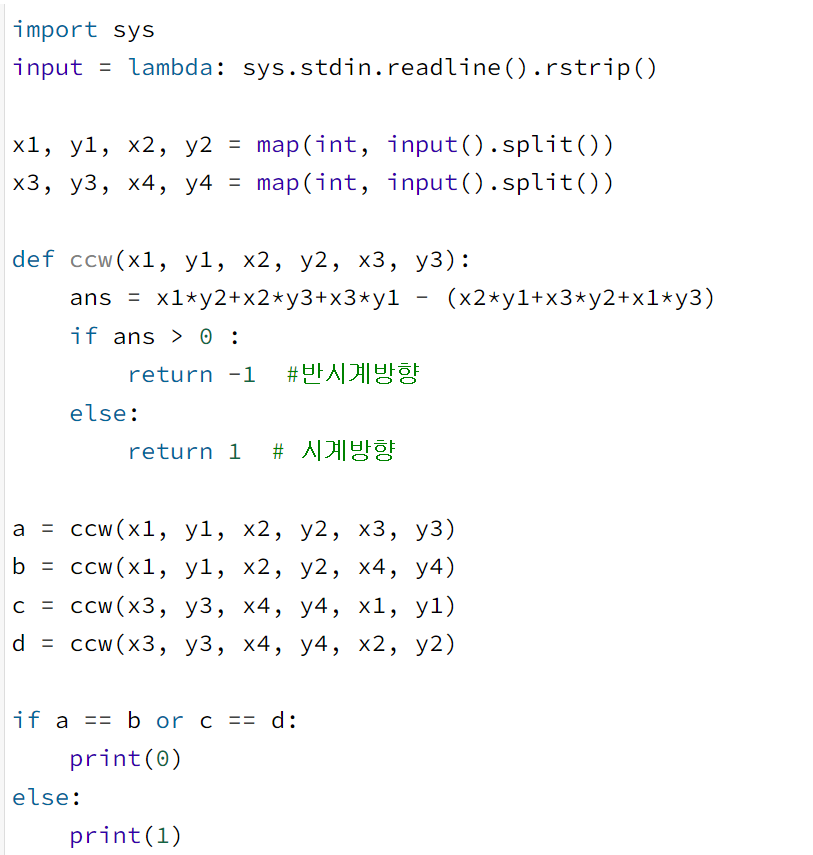
이 네 가지 경우를 제외하는 방법을 코드로 나타내면 아래와 같다.
♣ 백준 알고리즘 17387번(선분교차2)
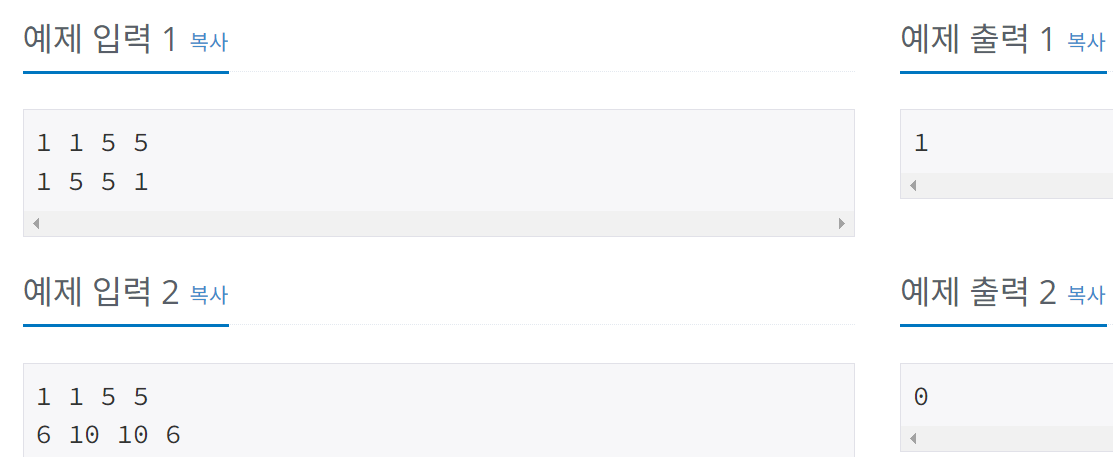
이번 문제는 한 선분의 끝 점이 다른 선분이나 끝 점 위에 있는 경우도 포함하는 문제이다. 즉 위에서 인정했던 경우의 수(한 선분에 대해 다른 선분의 한 점은 시계 방향에, 다른 한 점은 반시계 방향에 있을 것)에 더해서 한 선분 위에 다른 선분의 한 점이 있는 경우도 교차하는 것으로 인정한다.
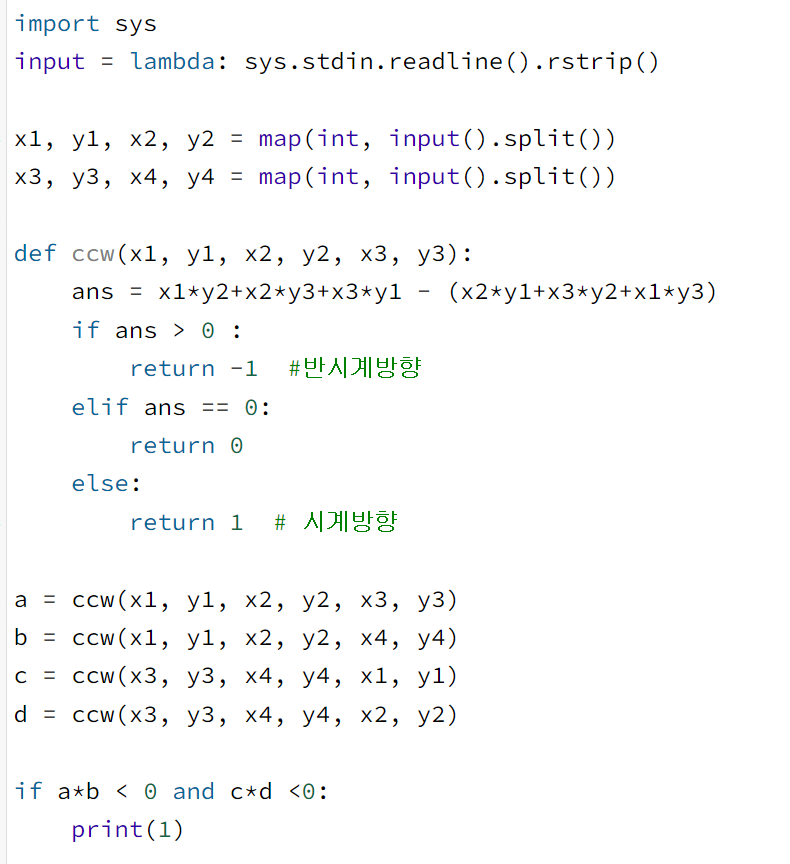
먼저, 첫 번째 문제와는 조금 달리 ans==0 인 경우도 ccw 함수에 넣는다. 그리고 네 가지 경우(a, b, c, d)를 계산한다.
a*b < 0 이면서 c*d < 0 이면 아래 그림처럼 두 개 선분이 서로 완전히 교차한 경우를 의미한다.

완전히 교차한 경우는 구하였으므로 이제 한 선분 위에 다른 선분의 점이 존재해서 교차로 인정되는 경우만 찾으면 된다.
x1, y1 - x2, y2 위에 x3, y3 점이 존재하는지 알아본다고 하자. ccw(x1, y1, x2, y2, x3, y3)를 실행해서 0이 return 되더라도 x3, y3가 x1, y1 - x2, y2 선분 위에 있는지는 알 수 없다. 그 위에 존재하지 않아도 선분 x1, y1 - x2, y2 을 연장한 가상의 직선 위에 x3, y3가 존재한다면 0이 return 되기 때문이다.
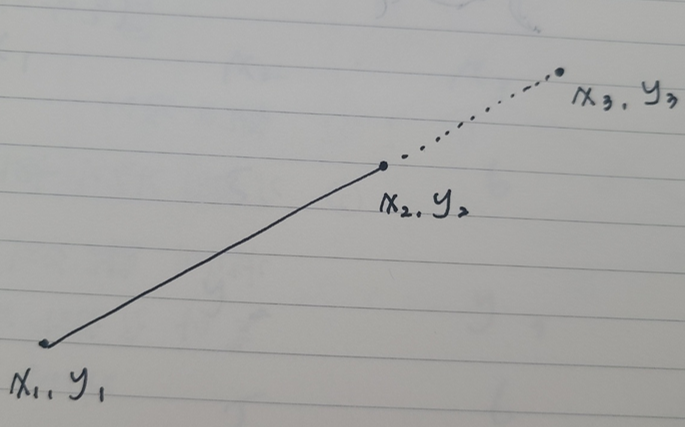
따라서 확실하게 x3, y3가 x1, y1 - x2, y2 선분 위에 존재하는지 구해야 한다.
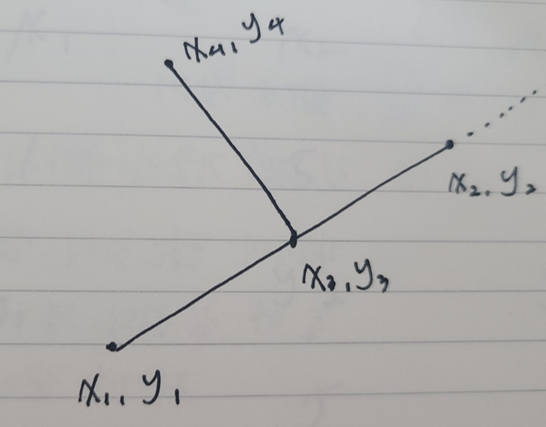
위의 그림을 보면 x3는 x1과 x2 사이에 있다. 또한 y3는 y1과 y2보다 사이에 있다. 이런 경우에는 확실하게 x3, y3가 선분 위에 존재한다고 판단할 수 있다.
이렇게 선분 위에 점이 존재하는 경우를 판별하기 위해 아래와 같이 코드를 만든다.

한 점이 한 선분 위의 두 점 사이에 존재하는지 판단하는 find 함수를 만들어서 네 가지 경우를 판별한다.
1) x1, y1 - x2, y2 위에 x3, y3 가 있을 때
2) x1, y1 - x2, y2 위에 x4, y4 가 있을 때
3) x3, y3 - x4, y4 위에 x1, y1 이 있을 때
3) x3, y3 - x4, y4 위에 x2, y2 가 있을 때
두 선분이 완전히 교차하는 경우, 한 선분 위에 다른 선분의 점이 존재하는 경우를 모두 구하고 그 어디에도 포함되지 않는 경우는 두 선분이 만나지 않는 것으로 판단하여 0을 출력한다.

CCW 알고리즘을 알면 그리 어렵지 않게 풀 수 있는 문제들이었다.
'알고리즘' 카테고리의 다른 글
| 데이크스트라 알고리즘(백준 알고리즘 13549번) (0) | 2024.08.12 |
|---|---|
| 유니온 파인드/분리집합 알고리즘(백준알고리즘 1043번) (0) | 2024.07.25 |
| 분할정복(백준 알고리즘 5904번) (0) | 2024.06.20 |
| 분할정복(백준 알고리즘 10830번) (0) | 2024.06.06 |
| 비트마스킹(백준 알고리즘 2961번) (0) | 2024.05.21 |