2024. 12. 12. 19:42ㆍ알고리즘
♠ 문제 이해

주어진 n을 이용하여 그래프를 만들어서 가로, 세로축에 따라 어떤 숫자가 나오는지를 계산하면 해결할 수 있는 문제이다. 0, 0 위치에 1이 들어가고, 대각선 방향으로 숫자가 점점 커지며 들어가는 규칙이 있다.
♠ 수학적 알고리즘 정리
우선 가로, 세로에 따라 해당 칸의 숫자를 구하는 수학 알고리즘을 정리해보았다.

n = 4 일 때의 행렬을 그려보았다. 가로를 i, 세로를 j 라고 생각해서 위의 행렬을 가로, 세로 크기로 나타내면 아래와 같다.

1) 윗부분의 숫자 구하기
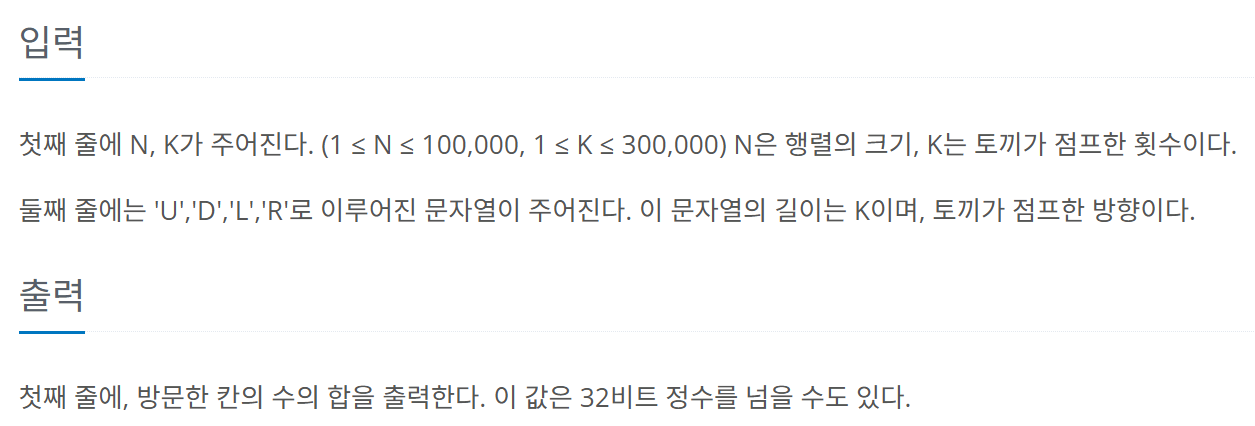
대각선으로 자르면 각 구간에서 i+j의 합이 같다. i + j = 0 인 구간에서 i + j = 3 인 구간까지를 행렬의 '윗부분'이라고 생각할 때, 각 구간의 첫 번째 수를 구하는 알고리즘은 아래와 같다.
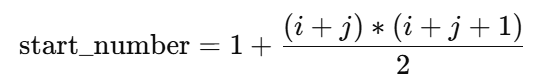

| i+j | 0 | 1 | 2 | 3 |
| start_number | 1+ 0*1//2 = 1 | 1 + (1)*(1+1)//2 = 2 |
1+2*3//2 = 4 |
1 + 3*4//2 = 7 |
각 구간의 첫 번째 숫자를 구했다. 이 숫자를 알면 같은 구간의 다른 숫자를 구할 수 있다.
① 홀수 대각선 구간에서 다른 숫자 구하기
i + j = 3 인 홀수 대각선 구간에서 start_number를 이용하여 다른 칸의 숫자를 구하려고 한다.
i + j = 3 인 구간에서 각 칸의 i, j 는 다음과 같다.
| i | 3 | 2 | 1 | 0 |
| j | 0 | 1 | 2 | 3 |
| number | 7 (start_number) | 8 | 9 | 10 |
start_number 다음 숫자부터 보면 start_number에 j를 더한 값이 number 가 된다는 것을 알 수 있다.
이는 i + j = 1 인 홀수 대각선 구간에서도 마찬가지이다.
| i | 1 | 0 |
| j | 0 | 1 |
| number | 2 | 3 |
여기서도 start_number 다음 숫자를 보면 start_number에 j를 더한 값이 number가 된다.
따라서 i + j = 홀수 인 대각선 구간에서 각 칸의 숫자를 구하는 알고리즘은 다음과 같다.

② 짝수 대각선 구간에서 다른 숫자 구하기
i + j = 짝수 인 구간에서는 홀수에서와 달리 i 를 이용한다.
i + 2 = 2 인 구간에서 start_number를 이용하여 다른 칸의 숫자를 구할 수 있다.
| i | 0 | 1 | 2 |
| j | 2 | 1 | 0 |
| number | 4 | 5 | 6 |
start_number 다음 숫자부터 보면 start_number에 i를 더한 값이 number 가 된다는 것을 알 수 있다.
따라서 i + j = 짝수 인 대각선 구간에서 각 칸의 숫자를 구하는 알고리즘은 다음과 같다.
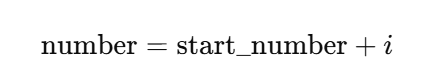
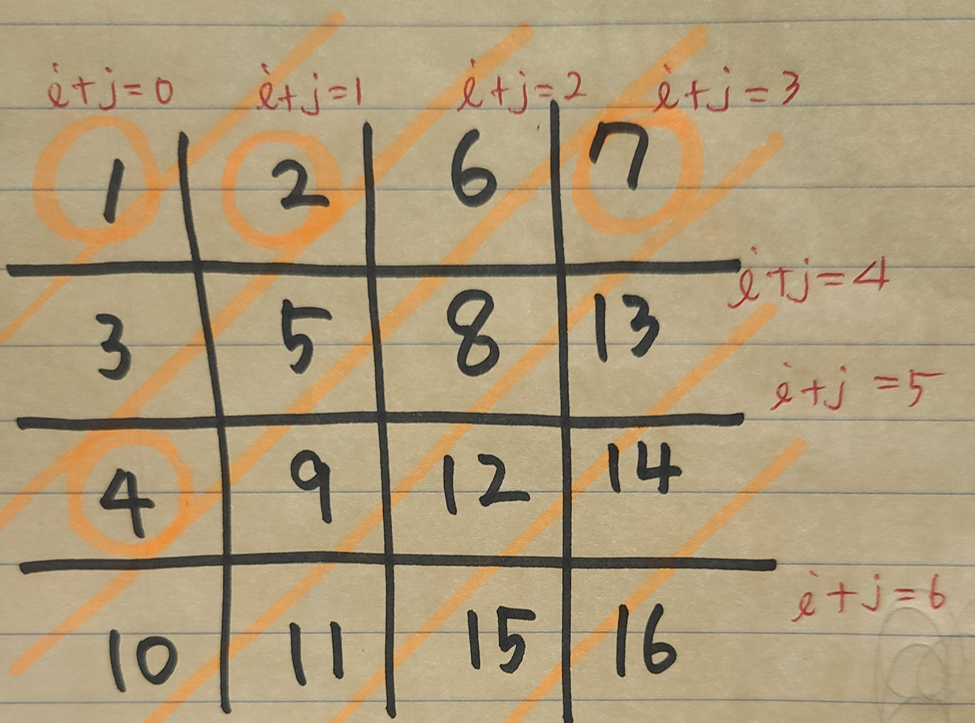
문제는 i + j = 4 부터 시작하는 아랫부분, 즉 숫자의 수가 줄어드는 구간부터는 이 알고리즘이 적용되지 않는다는 점이다.
start_number 를 위에서 이야기한 알고리즘을 사용하여 계산하면 1 + 5*6//2 = 16 이 되어서 i + j = 5 구간의 첫 번째 숫자인 14와 들어맞지 않는다. 따라서 숫자가 줄어드는 아랫부분에서는 새로운 알고리즘을 적용해야 한다.
'알고리즘' 카테고리의 다른 글
| DP, 수학공식(백준 알고리즘 1892번) (0) | 2024.12.26 |
|---|---|
| 투포인터(백준 알고리즘 20442번) (0) | 2024.12.18 |
| 위상정렬(백준 알고리즘 14567번) (0) | 2024.11.20 |
| 누적합(백준 알고리즘 2015번) (0) | 2024.11.14 |
| 누적합(백준 알고리즘 10986번) (0) | 2024.11.06 |