2024. 3. 14. 20:44ㆍ알고리즘
♣ 문제 이해하기


♣ 문제 풀이
당연히 DP를 사용하는 문제이다. 포도주 세 잔을 연달아 마실 수 없을 때, 최대로 포도주를 마실 수 있는 방법을 찾아야 한다. 각 포도주 잔이 가진 양을 나타내는 배열을 drinks, 앞에서부터 마신 포도주를 적립한 양을 나타낸 배열을 dp라고 한다. 포도주를 마실 때마다 다음과 같이 선택할 수 있다.
1. i번째 포도주를 마실 때
1-1. i-1 번째 포도주를 마시지 않았을 때
i번째 포도주는 마시면서 i-1번째 포도주는 마시지 않았을 때, 최댓값을 구하려면 i-3번째 포도주와 i-2번째 포도주는 모두 마신 상태여야 한다.
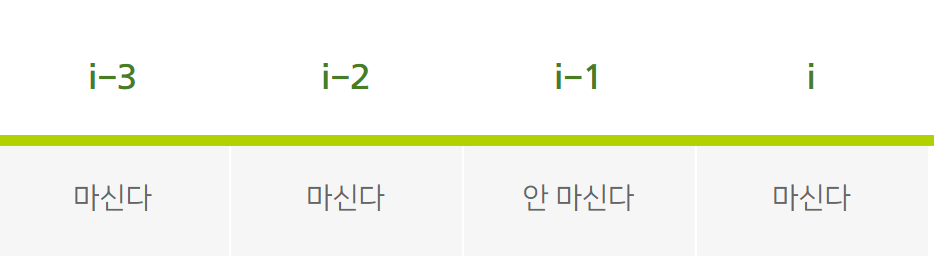
따라서 dp[i] =dp[i-2] + drinks[i]
1-2. i-1번째 포도주를 마셨을 때
i번째 포도주와 i-1번째 포도주를 모두 마실 때는 세 잔을 연달아 마시면 안되므로 i-2번째 잔의 포도주는 마시면 안된다.
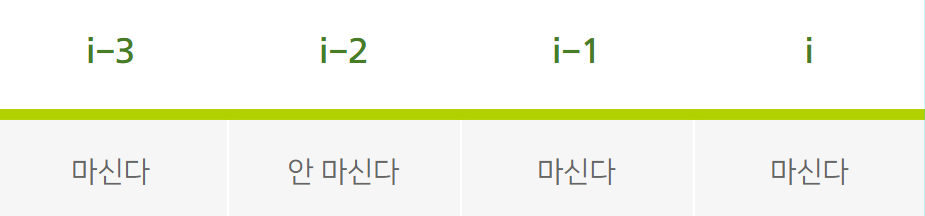
dp[i] = dp[i-3] + drinks[i-1] + drinks[i]
그런데 왜 dp[i-1] + drinks[i] 로 쓰면 틀리는 걸까? 왜냐하면 dp[i-1]이라면 i-1 번째 포도주를 마실 때의 최댓값이기 때문에 dp[i-2]에서 포도주를 마시지 않았다는 확신이 없기 때문이다. 즉 i-1번째, i-2번째 포도주를 마시고 i-3번째 포도주를 마시지 않은 상태일 수도 있다는 것이다. 그러면 i번째 포도주를 마시지 않아야 해서 조건이 달라진다.
2. i번째 포도주를 마시지 않을 때
i번째 포도주를 마시지 않는 경우도 존재한다. 이때는 dp[i] = dp[i-1]과 같다.
위의 세 가지 경우의 수 1-1, 1-2, 2 중 값이 가장 큰 것을 고르면 된다.
♣ 전체 코드

주어진 포도주가 2잔까지일 때는 두 잔 모두 마시는 게 이득이므로 sum(drinks)를 출력한다.
'알고리즘' 카테고리의 다른 글
| 백트래킹(백준 알고리즘 1987) (0) | 2024.03.29 |
|---|---|
| 애드훅(ad-hoc, 백준 알고리즘 31631번) (0) | 2024.03.22 |
| 다각형의 넓이 구하기(백준 알고리즘 2166번) (0) | 2024.03.06 |
| CCW(Counter Clock Wise, 백준 알고리즘 11758번) (0) | 2024.02.26 |
| 순열(백준 알고리즘 10973번) (0) | 2024.02.21 |