2024. 3. 22. 20:32ㆍ알고리즘
♣ 애드훅
라틴어로 'for this particular purpose'라는 뜻으로, 특정 상황에서만 정답이 되고 일반화될 수 없는 해답을 의미한다.
정형화된 방법론이 아니라 그 문제를 풀기 위한 창의적인 아이디어를 떠올려야 하는 경우를 애드훅 문제라고 한다.
따라서 코드를 재사용하는 것이 거의 불가능하다. 최적의 선택이 아니므로 개발 기간이 촉박할 때 급하게 요구 사항을 맞추는 데 사용된다.
♣ 백준 알고리즘 31631번

♣ 문제 이해
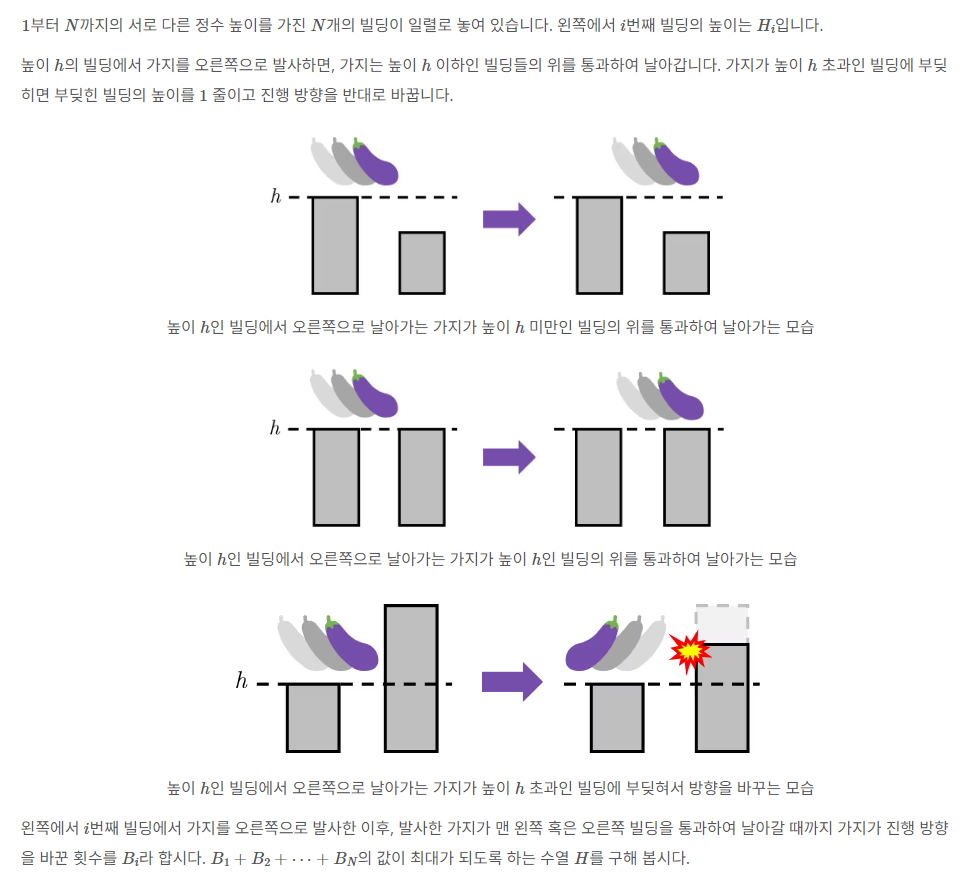
빌딩의 숫자가 주어졌을 때, 빌딩 위로 가지를 날리는데 가지의 방향을 가장 많이 바꿀 수 있는 경우를 구하는 문제이다.
가지는 1번 건물에서부터 오른쪽으로 날아가기 때문에 맨 오른쪽 건물이 가장 높아야 한다. 그리고 나서 왼쪽과 오른쪽에 번갈아서 큰 건물을 넣는다.
1 2
2 1 3
3 2 1 4
4 3 1 2 5
5 4 1 2 3 6
이런 식으로 오른쪽에 가장 높은 건물이 들어가면 그 다음 높은 건물은 맨 왼쪽에 들어가고, 맨 왼쪽의 다음 건물이 그 다음으로 높은 건물이 된다. 이렇게 오른쪽과 왼쪽을 주고받으면서 건물을 배치하면 가지가 방향을 가장 많이 바꿀 수 있다.
♣ 문제 해결

빌딩의 높이를 규칙에 맞게 배치하기 위해서 건물을 세우는 위치를 token으로 표시한다. 또한 first는 맨 마지막 건물의 위치를, last는 맨 첫 건물의 위치를 의미한다. 맨 마지막 건물의 높이가 가장 높아야 하기 때문에 first를 n-1로 설정했다. token이 0일 때는 오른쪽 건물을 세울 때라고 가정한다. 따라서 현재의 오른쪽 건물(first)에는 지금으로써 가장 높은 높이(i)의 건물을, 반대의 왼쪽 건물(last)에는 지금으로써 두 번째로 높은 높이의 건물(i-1)을 설정한다. 이렇게 오른쪽-왼쪽 순서로 건물을 올린 다음에는 반대로 왼쪽-오른쪽 순서로 건물을 올려야 한다.
따라서 token을 1로 바꿔서 이번에는 왼쪽 건물(last)에 현재로써 가장 높은 건물(높이 i)을 올린다. 그리고 오른쪽 건물(first)에는 그 다음으로 높은 건물(높이 i-1)을 올린다. 그리고 다시 token을 0으로 바꿔서 오른쪽 건물부터 올리면 된다.
그런데 이렇게 하다보면 한 번에 두 개씩 건물을 올리게 되므로 건물이 홀수 개 있을 때 맨 가운데 건물의 높이가 0이 되어 버린다. 따라서 이렇게 buildings 높이에 0이 있을 경우에는 그 건물의 높이를 1로 해서 가장 작은 건물로 바꾸어주면 된다.
♣ 참고 자료
https://jake-seo-dev.tistory.com/473
프로그래밍에서 말하는 애드혹 (ad-hoc, adhoc) 이란?
프로그래밍에서 말하는 애드혹 (ad-hoc, adhoc) 이란? 라틴어로 "for this particular purpose" 이다. 특정 상황에서만 정답이 되고 일반화될 수 없는 해답을 말한다. 그러므로 재사용되는 것이 거의 불가능
jake-seo-dev.tistory.com
'알고리즘' 카테고리의 다른 글
| 투 포인터(백준 알고리즘 1644번) (0) | 2024.03.31 |
|---|---|
| 백트래킹(백준 알고리즘 1987) (0) | 2024.03.29 |
| DP(백준 알고리즘 2156번) (0) | 2024.03.14 |
| 다각형의 넓이 구하기(백준 알고리즘 2166번) (0) | 2024.03.06 |
| CCW(Counter Clock Wise, 백준 알고리즘 11758번) (0) | 2024.02.26 |