2023. 8. 7. 13:04ㆍCNN
Chapter1
Introduction
최근 이미지넷 이미지 분류 챌린지에서 최신 기술을 능가하는 데 깊은 합성곱 신경항(Deep CNN)이 사용됨
CNN의 출력은 입력 데이터의 형태, 커널의 형태, 제로패딩, 스트라이드에 의해 영향을 받음. 한편 이런 속성들 사이의 관계는 단순하게 추론하기 어려움.
-입력 데이터의 형태: 입력이미지의 크기, 채널 수
-커널의 형태: 커널의 크기, 채널 수
CNN은 fully-connected layers(완전연결층)와는 다름. fully-connected layers의 출력 크기는 입력 크기와는 독립적임.
-CNN vs fully-connected layers
1. 완전연결층의 출력 크기는 입력 크기와 독립적으로, 항상 일정한 크기의 출력을 생성함.
2. CNN는 합성곱레이어와 함께 풀링레이어를 주로 사용함. 풀링레이어는 합성곱레이어에서 추출한 feature map의 크기를 줄이는 역할을 수행함. 주로 최대 풀링(Max Pooling)이나 평균 풀링(Average Pooling)이 사용되며 이로 인해 네트워크의 크기가 줄어들고 계산량이 감소함.
-CNN은 이미지와 같은 공간적인 구조를 가진 데이터에서 뛰어난 성능을 보이지만, 그에 따른 복잡성이 증가함. 이미지에서는 지역적인 특징들이 중요하므로 커널을 사용하여 합성곱을 수행하고, feature map을 생성함. 또한 풀링 레이어를 통해 공간적인 크기를 줄이면서 중요한 정보를 보존함. 이와 달리 완전 연결층은 각 뉴런들이 모든 입력과 연결되어 각각의 입력과 가중치를 고려하는데, 이로 인해 가중치가 많이 증가하고 연산량이 많아짐.
-따라서 CNN은 복잡한 이미지 데이터에 적합하며, 특히 이미지 분류와 객체 감지 등의 컴퓨터 비전 작업에서 많이 사용됨.완전 연결층은 일반적인 인공 신경망 구조에 주로 사용되며, 간단한 입력과 출력 크기를 다루는 경우에 적합함.
이 가이드의 역할
1. 합성곱 레이어와 전치 합성곱 레이어 사이의 관계 설명하기
: 합성곱 레이어와 전치 합성곱 레이어는 딥러닝에서 주로 이미지 처리와 관련된 작업에서 사용되는 두 가지 유형의 레이어 이들은 서로 역의 관계에 있으며, 주로 이미지 처리에서 특징 맵(feature map)을 추출하고 재구성하는 데 사용됨
- 합성곱 레이어: 합성곱 레이어는 입력 데이터와 학습 가능한 필터(또는 커널) 간의 합성곱 연산을 수행하여 특징 맵을 추출함. 이를 통해 이미지의 지역적인 특징이 감지되고, 이러한 특징들이 고차원의 특징으로 변환됨
- 전치 합성곱 레이어: 전치 합성곱 레이어는 합성곱 레이어와 반대로 작동. 합성곱 레이어와는 다르게 입력 데이터에 학습 가능한 필터를 적용하고, 더 큰 특징 맵을 생성하여 이미지를 확장하는 역할을 수행. 이로 인해 특징의 크기가 원래 입력의 크기보다 큰 이미지를 얻을 수 있음.
2. 입력 형태, 커널 형태, 제로패딩, 스트라이드와 출력 형태를 직관적으로 이해하기
1.1 Discrete convolutions(이산 합성곱) = 그냥 합성곱이라고 생각해도 될 듯
신호 처리와 딥러닝에서 주로 사용되는 연산. 두 개의 이산 신호(데이터) 사이에서 필터를 슬라이딩하며 각 위치에서 합성곱 연산을 수행하는 것을 의미함. 입력 신호와 필터 사이의 상호작용을 통해 새로운 출력 신호를 생성.
신경망의 기본은 선형 변환(affine transformations)임. 선형 변환은 벡터를 입력으로 받아서 행렬과의 곱셈을 통해 출력을 생성. 이 변환은 이미지, 음성 클립 또는 순서 없는 특징들의 모음과 같은 어떤 종류의 입력에 적용 가능함.
이미지, 음성 클립 및 다른 유사한 종류의 데이터들이 공유하는 중요한 속성들
- 데이터들은 다차원 배열로 저장됨
- 데이터들은 하나 이상의 축(axis)을 가지며, 그 중 몇 개의 축은 순서가 중요함. 예를 들어 이미지의 경우 폭( width)와 높이(height)축이 있으며, 음성 클립의 경우 시간(time) 축이 있음.
- 채널 축은 데이터의 다른 관점에 접근하는 데 사용됨. 예를 들어 컬러 이미지의 경우, 빨, 초, 파의 다양한 관점을 표현하고 스테레오 오디오 트랙의 경우 좌우 채널 등을 가질 수 있음.
이러한 속성들은 선형 변환을 적용할 때 할용되지 않음.
이산 합성곱은 합성곱레이어에서 사용되는 기본적인 연산으로, 이미지 처리와 같은 공간 구조를 가진 데이터에서 특징을 추출하는 데 유용함. 이러한 합성곱 레이어는 입력과 커널 사이에서 합성곱 연산을 수행하며 공간적인 특징을 추출하고 이를 효과적으로 활용함.
이산합성곱의 특징
1. 순서 보존: 이산 합성곱은 입력과 커널(필터) 사이에서 합성곱 연산을 수행하여 출력을 생성함. 이 과정에서 입력의 순서에 따른 구조와 특성들이 보존됨.
2. 희소성: 이산 합성곱은 일부 입력 단위만이 특정 출력 단위에 영향을 미치므로, 입력과 출력 간의 연결이 희소한 구조를 가짐.
3. 파라미터 재사용: 이산 합성곱에서는 동일한 가중치(필터)가 입력의 여러 위치에서 재사용됩니다. 이는 필터가 여러 위치의 특징을 감지하는 데 도움이 되며, 학습해야 하는 파라미터의 수를 크게 줄여줌.
이미지 하나에 커널 하나(가중치 하나)를 사용하는 예시
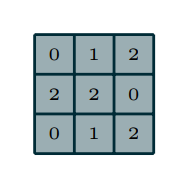


5X5 input에 3X3 커널 적용. 1X1의 제로패딩과 2X2의 스트라이드 적용한 예시
주목할 점은 strides(스트라이드)는 하위 샘플링(subsampling)의 형태를 구성한다는 점. 스트라이드는 커널이 얼마나 이동하는지의 척도로 해석되는 대신, 출력의 얼마나 많은 부분이 보존되는지로도 볼 수 있음. 예를 들어, 커널을 두 칸씩 이동시키는 것은 커널을 한 칸씩 이동시키되 홀수 위치의 출력 요소만 보존하는 것과 동일함(Figure 1.4)

스트라이드의 특성은 커널의 이동에 따른 출력의 크기와 관련하여 중요함. 적절한 스트라이드를 선택하여 원하는 출력 크기와 특성을 얻을 수 있으며, 이는 모델의 효율성과 정확성에 영향을 미치는 요소 중 하나임. 또한, 스트라이드를 이용하여 하위 샘플링을 수행할 수 있으며, 이는 모델의 계산 비용을 줄이고 공간적인 정보의 손실을 조절하는 데에 사용됨.
이미지 여러 개에 여러 개의 커널을 사용하는 예시
각 위치에서, 커널의 각 요소와 겹치는 입력 요소 간의 곱셈이 계산되고, 결과들이 합산되어 현재 위치의 출력이 얻어짐.
이 프로세스는 서로 다른 커널을 사용하여 원하는 만큼의 출력 특징 맵을 형성하는 데 반복해서 적용될 수 있음(Figure 1.3). 이러한 절차의 최종 출력은 출력 특징 맵(output feature maps)이라고 함.

만약 여러 개의 입력 특징 맵이 있는 경우, 커널은 3차원이어야 함. 즉, 각 입력 특징 맵마다 서로 다른 커널과 합성곱이 수행되며, 이러한 결과 특징 맵들은 원소별로 합산되어 출력 특징 맵을 생성함.
커널은 학습 가능한 가중치로서, 합성곱 레이어는 이러한 가중치를 통해 자동으로 학습하며 입력 데이터에서 유용한 특징을 감지하는 데 사용됨. 여러 개의 커널을 적용하면 다양한 특징을 추출하는 데 도움이 되며, 이를 통해 딥러닝 모델이 다양한 문제를 해결하는데 더욱 효과적으로 활용함.
위의 Figure 1.3은 두 개의 입력 특징 맵에서 세 개의 출력 특징 맵으로의 합성곱을 나타내는 것으로, 3 × 2 × 3 × 3 크기의 커널 w를 사용함
- 3: 합성곱 연산에 의해 생성되는 출력 특징 맵(출력 채널)의 개수. 집합 내 각 커널은 하나의 출력 특징 맵을 생성함. 커널의 수를 의미하기도 함.
- 2: 이는 합성곱 연산에 사용되는 입력 특징 맵(입력 채널)의 개수를 나타냄. 집합 내 각 커널은 두 개의 입력 특징 맵을 받아와서 합성곱을 수행함.
- 3 × 3: 이는 집합 내 각 커널의 크기를 나타냄. 이 경우, 각 커널의 크기는 3 × 3이며, 즉 3 x 3 행렬로 구성되어 있음.
즉 Figure 1.3에서는 3 x 3 크기의 커널 3개를 사용하며, input 데이터(채널)은 2개, output 데이터(채널)은 3개임.
3개의 각 커널이 input data와 합성곱하는데, input channel이 2개 이므로 각 커널이 weight(가중치)를 2개 세트 가지고 있어야 함. 그래야 각 input과 weight를 곱해서 feature map을 만듦.
3 x 3 크기의 커널이므로 한 개 커널 당 weight가 9개씩 들어있고, 각 커널이 가중치를 2개 세트 가지고 있으니까 weight는 9 x 2로 18개. 여기다가 채널이 3개이니까 18 x 3까지 하면 총 가중치의 개수를 알 수 있음.
왼쪽 경로에서는 입력 특징 맵 1이 커널 w1,1과 합성곱을 수행하고, 입력 특징 맵 2는 커널 w1,2와 합성곱을 수행하여 결과를 원소별로 합산하여 첫 번째 출력 특징 맵을 형성함. 중간과 오른쪽 경로에서도 동일한 과정을 반복하여 두 번째와 세 번째 특징 맵을 형성하고, 이 세 개의 출력 특징 맵은 모두 하나로 묶여서 출력을 형성함. 즉 output channel이 3이긴 하지만 결국 모든 feature map을 합쳐서 하나의 결과를 가져옴.
각각의 feature map을 쌓으므로 3차원 데이터가 된다.
1.2 Pooling
합성곱 외에도 pooling 연산은 CNN에서 또 다른 중요한 구성 요소임. pooling 연산은 하위영역을 요약하는데, 어떤 함수를 사용하여 feature map의 크기를 줄이는 데 사용됨. 주료 평균(Average Pooling)이나 최댓값(Max Pooling)을 취하는 방식으로 수행됨.
pooling 연산의 주된 목적
1. Spatial Downsampling(공간적인 다운샘플링): pooling 연산은 feature map의 크기를 줄임으로써 계산 비용을 줄이고 메모리 사용을 최적화하는 데 기여함. 특히 대규모 이미지 처리에서 중요한 역할을 함. pooling을 통해 feature map의 해상도를 낮추는 것은 일부 공간적인 정보의 손실을 가져울 수 있지만 중요한 특징들은 여전히 유지되므로 학습에 영향을 미치는 정확도를 크게 감소시키지 않음
2. Variability to Location(위치 변동성): pooling 연산은 특징의 위치 변동성을 완화하는 데 도움됨. 합성곱 연산에서는 커널이 입력 데이터 위에서 이동하는 것에 따라서 특징이 감지되는 위치가 달라질 수 있음. 하지만 pooling 연산은 작은 하위 영역들을 요약하여 대표값을 구하므로 특정 위치에 대한 강건성을 갖게됨. 이를 통해 특징의 위치 변동성에 대한 영향을 줄이고 모델의 일반화 능력을 향상시킴.
Pooling 작업은 입력 데이터 위에서 창(window)를 슬라이딩하면서 창 내용을 풀링 함수에 전달하는 방식으로 동작함. 합성곱과 매우 유사하게 작동하지만, 커널이 실행하는 선형 조합을 다른 함수로 대체함.
Pooling 레이어의 출력 크기에 영향을 미치는 파라미터들
1. ij: 축 j에 따른 입력 크기
2. kj: 축 j에 따른 풀링 창(window) 크기
3. sj: 축 j에 따른 스트라이드 값


Chapter2
Convolution arithmetic(합성곱 산술: feature map의 크기 계산)
신경망의 합성곱층에서 발생하는 출력 feature map의 크기를 계산하는 과정을 의미함. 이 과정은 입력, 커널, 스트라이드, 제로패딩, 확장(dilation)과 같은 속성을 기반으로 출력 feature map의 차원을 결정하는 작업을 포함함.
* i = input channel, s = stride, p = padding, k = kernel, o = output
합성곱이 끝난 후의 feature map의 크기를 계산해보자
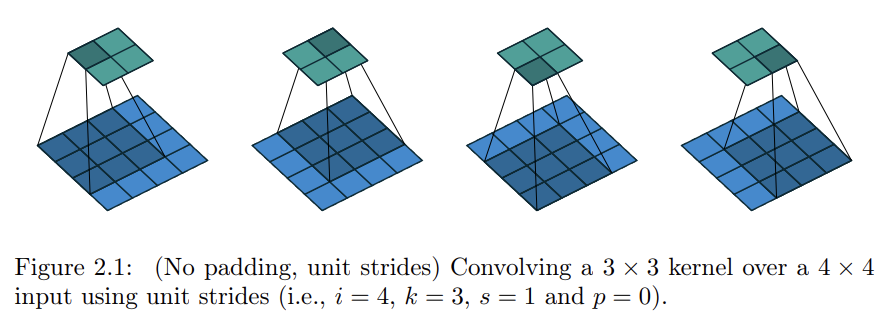
2.1 No zero padding, unit strides(0으로 채워진 padding 없음, stride는 1)
합성곱의 가장 간단한 분석. 이 경우, 커널은 input feature mpa의 모든 위치를 한 칸씩 이동하면서 슬라이딩됨.
-output feature의 가로축: 출력의 크기는 커널이 input의 끝에 닿을 때까지 가는 칸의 갯수 + 1임
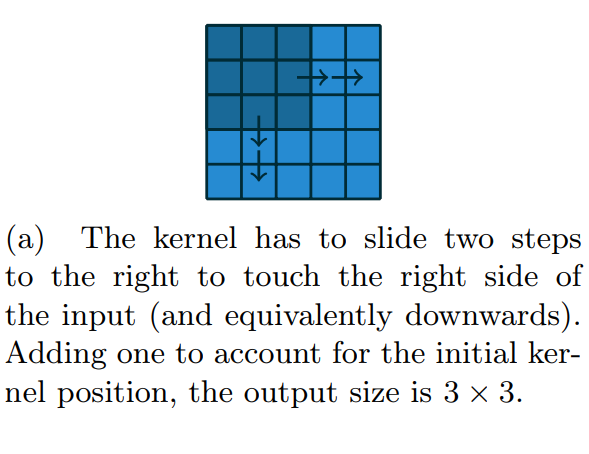
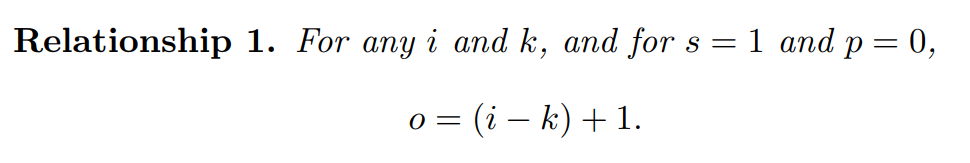
* o는 출력의 크기, i는 input feature의 크기, k는 커널의 크기.
위의 그림에 대입하면 o = (5-3)+1 이니까 output feature map의 크기가 3이 됨.
2.2 Zero padding, unit strides(제로 padding 사용, stride 1)
p개의 제로 패딩을 추가하면 유효한 input 크기는 i에서 i + 2p로 변경됨. 왜냐하면 패딩이 양쪽에 생기니까 제로 패딩이 1이면 입력의 크기가 양쪽으로 1씩 늘어나서 2배가 됨.
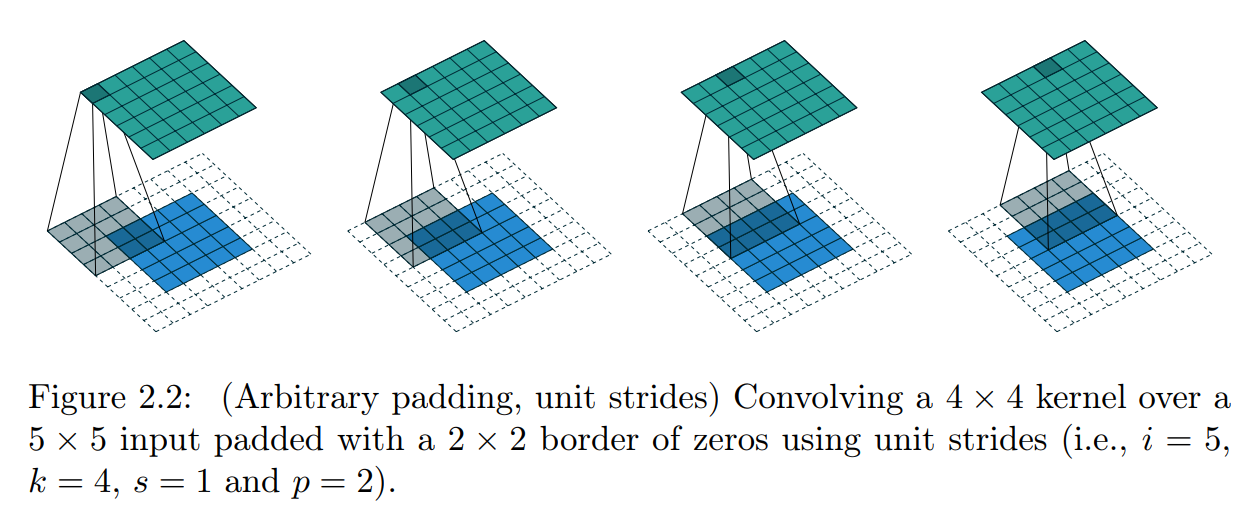
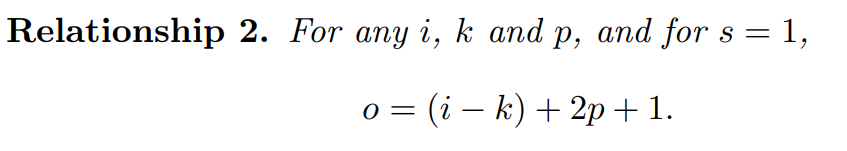
위의 그림에 적용하면 o = (5-4) + 2x2 + 1 = 6. 즉 output의 크기는 6임.
2.2.1 Half(same) padding
반 padding으로 출력 크기를 입력 크기와 동일하게 유지하기


위의 그림에 적용하면 o = 5 로 입력 크기와 출력 크기가 동일하게 유지됨. 커널의 크기가 홀수인 경우에 해당함.
이러한 방식은 반(half) padding 또는 동일(same) padding이라고도 불림.
2.2.2 Full padding
합성곱을 할 때 일반적으로 출력 크기가 입력 크기보다 작아지지만, 때로는 그 반대가 필요할 수 있음. 그 경우를 나타냄. 적절한 제로 패딩과 커널을 이용하여 달성할 수 있음.
커널을 입력 feature map에 대해 가능한 모든 부분 또는 완전한 겹침을 고려하기 때문에 full padding이라고 함.


위의 그림에 적용하면 o = 5 + 2(3-1) - (3-1) = 5 + (3-1) = 7. 즉 출력의 크기가 7로 입력의 크기보다도 커짐.
2.3 No zero padding, non-unit strides(제로 padding 없음, stride는 1이 아님)
앞의 경우는 모두 stride=1인 합성곱에 해당했음. stride가 1이 아닌 경우에 대한 계산을 위해서는 다른 식이 필요함.
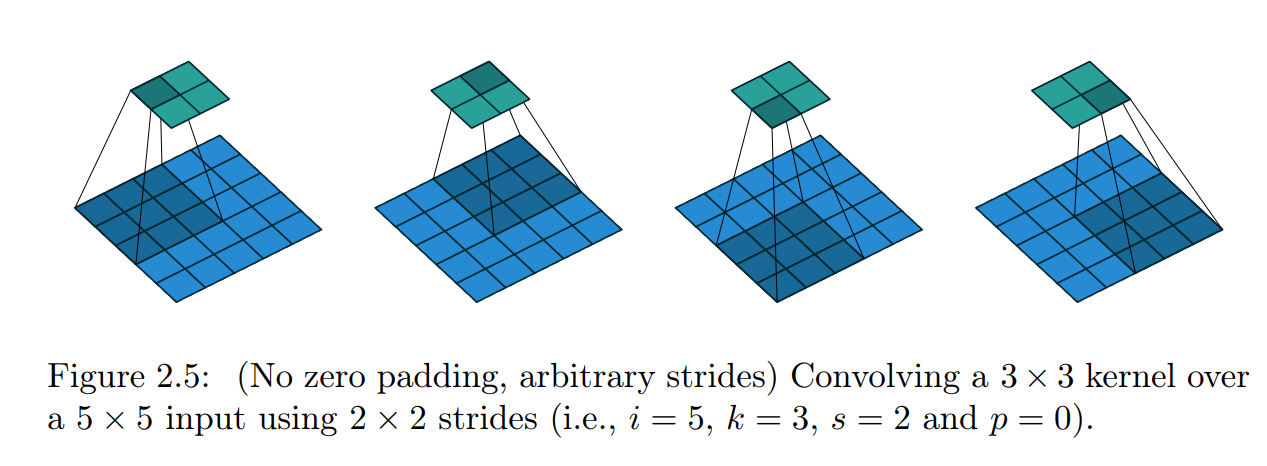
커널은 일반적으로 입력의 가장 왼쪽에서 시작하지만, 이번에는 크기 s로 슬라이딩하면서 입력의 오른쪽 끝에 닿을 때까지 이동함. 출력의 크기는 이동한 횟수에 1을 더한 값과 같음.

위 식에서 ⌊ ⌋는 내림 함수를 나타냄. 이는 때로는 마지막 가능한 스텝이 커널이 입력의 끝에 도달하지 않을 수 있기 때문에 사용됨. 즉, 일부 입력 단위가 제외되는 경우가 있을 수 있음.
Figure 2.5의 경우 o = (5-3)/2 + 1 = 2.즉 출력의 크기가 2가 됨.
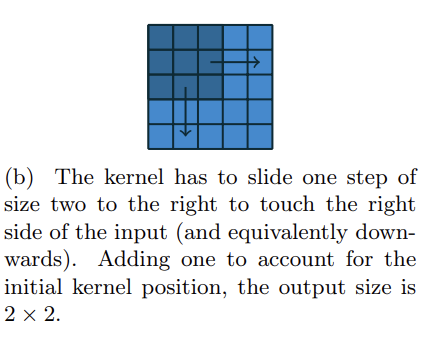
Figure 2.8b는 stride가 2인 경우. 커널이 input의 오른쪽 면에 닿으려면 1번(step) 이동함. 여기에 1을 더하면 output의 크기가 도출됨 => 2 x 2

Figure 2.7은 kernel이 input의 오른쪽 맨 끝까지 이동하지 못함. 위에서 말했던 대로 일부 입력 단위가 제외됨.
이 경우, 맨 오른쪽의 column과 가장 마지막에 있는 row는 kernel에 의하여 계산되지 못하고 제외됨.
위의 식에 적용하면 o = (8-3)/2 + 1임. input은 6이지만 여기에 padding을 더하면 w가 8이 됨. 여기서 (8-3)/2는 내림함수(버림)에 속하므로 2가 됨. 따라서 o는 3이므로 output의 크기는 3이 됨.
2.4 Zero padding, non-unit strides(제로 패딩 사용, stride는 1이 아님)
다양한 입력 크기를 가지더라도 stride, 제로 padding을 이용하여 합성곱은 동일한 출력 크기를 공유할 수 있음. 이는 합성곱에 대한 분석에는 영향을 미치지 않지만, 전치 합성곱의 경우 분석을 복잡하게 만들 수 있음.


위의 그림에 적용하면 o = (5 + 2 - 3)/2 + 1 => 2 + 1 = 3. 즉 output의 크기는 3임.
Figure 2.7도 여기에 예시로써 들어올 수 있음.
Chapter3
Pooling arithmetic
이전 장에서 다룬 합성곱 산술이 pooling 산술에도 적용될 수 있음. 풀링은 제로 패딩을 포함하지 않기 때문에, 일반적인 경우를 설명하는 관계식은 다음과 같음.

위의 관계식은 모든 유형의 pooling에 적용됨.
Chapter 4
Transposed convolution arithmetic(전치합성곱 산술)
전치 합성곱이 필요한 이유는 일반적으로 정상 합성곱과는 반대 방향으로 진행되는 변환을 사용하고자 하기 때문. 즉, 어떤 합성곱의 출력 형태에서 입력 형태로 변환하면서, 연결 패턴을 유지하며 해당 합성곱과 호환되는 형태로 변환하고자 할 때 사용됨. 예를 들어, 전치 합성곱은 합성곱 오토인코더의 디코딩 레이어로 사용하거나 특징 맵을 고차원 공간으로 투영하는 데 사용될 수 있음.
합성곱 케이스는 완전히 연결된 케이스(fully connected case)보다 훨씬 복잡함. 완전히 연결된 케이스는 단순히 형태가 전치된 가중치 행렬을 사용하는 것만으로 해결되지만, 합성곱은 효율적인 행렬 연산의 효율적인 구현으로 귀결되므로 완전히 연결된 케이스에서 얻은 통찰력이 합성곱 케이스를 해결하는 데 유용함. 합성곱 산술과 마찬가지로, 전치 합성곱 산술에 대한 논문은 전치 합성곱의 속성이 축 간에 상호 작용하지 않기 때문에 단순화되어 있음.
이번 chapter에서 다룰 주제들
• 2차원 전치 합성곱 (N = 2)
• 정사각형 입력 (i1 = i2 = i)
• 정사각형 커널 크기 (k1 = k2 = k)
• 양 축에서 동일한 스트라이드 (s1 = s2 = s)
• 양 축에서 동일한 제로 패딩 (p1 = p2 = p).
4.1 Convolution as a matrix operation(행렬 연산으로서의 합성곱)
예를 들어 Figure 2.1에서 나타난 합성곱에서 입력과 출력이 왼쪽에서 오른쪽으로, 위에서 아래로 벡터로 펼쳐진다면, 합성곱은 희소 행렬 C로 나타낼 수 있음. 여기서 비영(non-zero) 요소는 커널의 원소 wi, j임(i와 j는 각각 커널의 행과 열을 나타냄)

이 선형 연산은 입력 행렬을 16차원 벡터로 펼쳐서 처리하며, 그 결과로 4차원 벡터가 생성되고 나중에 이 벡터는 2 × 2 출력 행렬로 모양을 변경함.
16차원 벡터는 입력 행렬을 1차원으로 펼친 결과를 나타내며, 이 벡터의 각 요소는 각각 입력 행렬의 특정 부분과 커널의 합성 결과임. 이 결과 벡터는 커널의 개수에 따라 4차원이 되며, 이것이 나중에 2 × 2 출력 행렬로 모양을 변경함.
이해를 돕기 위해 추가적으로 설명드리면, 입력 행렬의 각 위치에서 커널을 적용하고, 그 결과로 얻은 값들을 모아 4차원 벡터로 만든 다음, 이를 다시 2 × 2 행렬 모양으로 변환함.
<희소 행렬 C에 대한 추가 설명>
행렬의 각 행은 출력 특징 맵 내의 특정 위치에 해당하며, 각 열은 펼쳐진 입력 특징 맵과 커널의 요소에 해당함. 커널의 요소는 w_i,j와 같이 표시되며, 여기서 i는 커널의 행을 나타내고 j는 커널의 열을 나타냄.
행렬 내의 0은 출력 특징 맵의 해당 위치에서 입력과 커널 간의 상호작용이 없는 경우를 나타냄. 이것은 합성곱이 커널을 입력 위로 슬라이딩하면서 일부 경우에는 커널의 일부가 입력과 겹치지 않을 수 있기 때문.
이 행렬은 합성곱이 어떻게 수행되는지와 출력 특징 맵의 각 요소가 입력과 커널 간의 상호작용을 통해 계산되는 방식을 시각화하는 데 도움이 됨.
이 표현을 사용하면 행렬 C를 전치(transpose)하여 역전파(backward pass)를 쉽게 얻을 수 있음. 즉, 오차는 손실을 CT와 곱하여 역전파됨. 이 연산은 4차원 벡터를 입력으로 받아 16차원 벡터를 출력으로 생성하며, 그 연결 패턴은 C와 호환됨
특히, 커널 w는 전방향과 역방향 전파에 사용되는 행렬 C와 CT 모두를 정의함
=> 왜 저런 C 행렬이 나오는지 이해되지 않는다면 <티스토리의 transposed convolution 설명2>를 읽어보자.
<티스토리의 transposed convolution 설명1>
보통의 convolution과 달리 전치합성곱은 upsampling을 함.
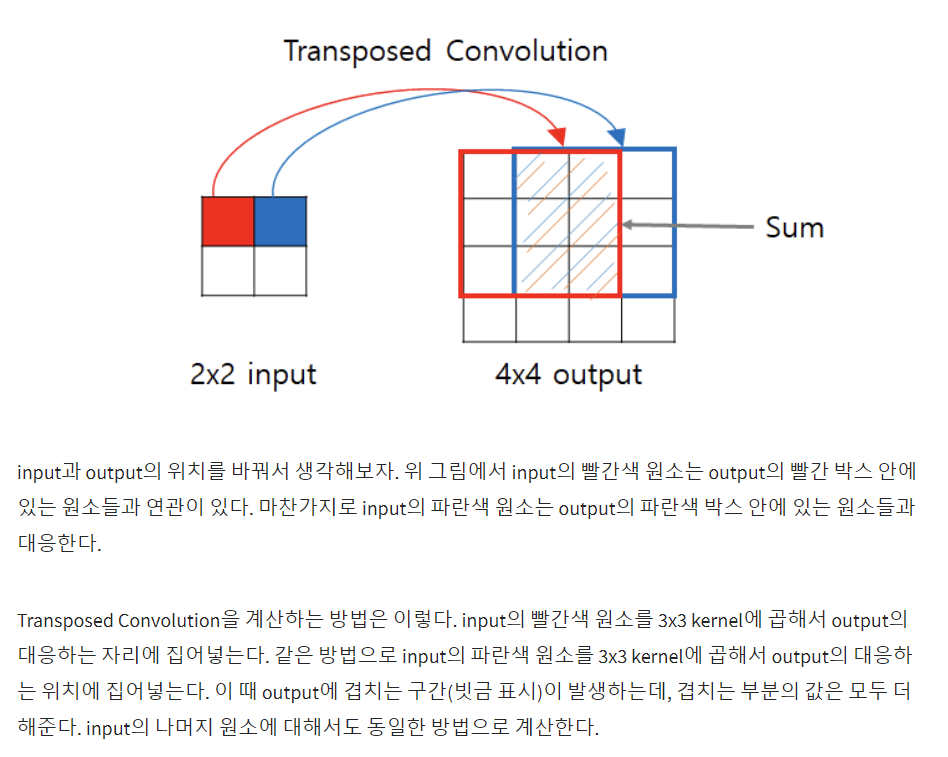
<티스토리의 transposed convolution 설명2>

<그림 1> Convolution 연산의 Input, kernel, Output

output 2 x 2 에서 4 x 4 로 만들어주는 과정. 값 1개로 9개의 값을 구함. 그 과정에서 기존에는 수학적 보간법들이 적용되었으나 transposed convolution은 학습을 통해 최적의 보간법을 학습함. 그림만 봐서는 어떤 연산에 의해 저런 값이 나오는지 알 수 없음. 이 연산을 위해 convolution matrix와 transposed convolution matrix를 정의해야 함.
convolution matrix
위에서 사용한 convolution kernel 은 3 x 3 사이즈이고 Input 영상은 4 x 4 이고 Output은 2 x 2임.
따라서 convolution matrix 를 4 x 16으로 만들어 줌.
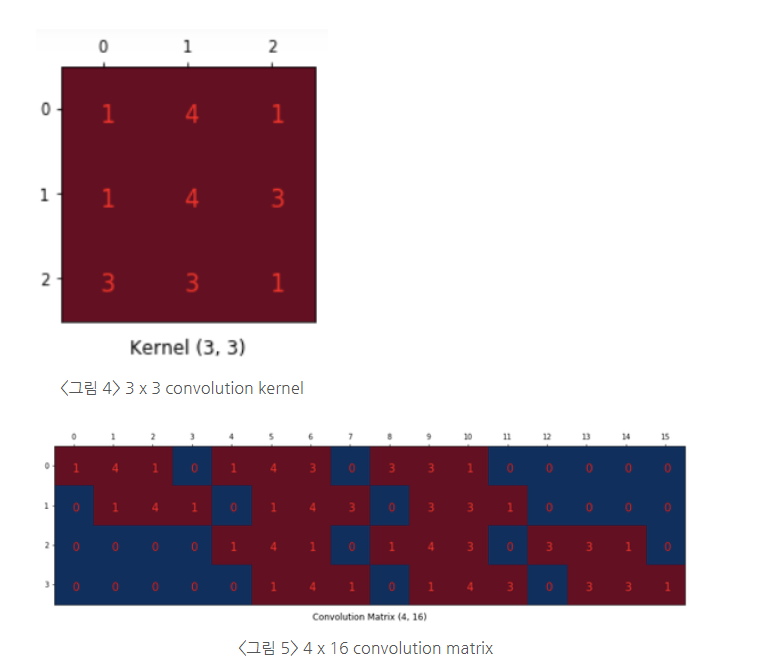
그림5의 1행은 4x4인 input 사이즈를 1 x 16으로 늘어놓은 것. 내부값은 무시함.
3 x 3의 kernel로 input에서 convolution 연산을 4번 진행했으므로 행이 4개가 됨. 그림5에서 1행은 convolution 연산이 처음 진행되었을 때 kernel이 적용되었던 위치를 넣은 것. kernel의 윗줄에서부터 가중치를 적용함. 한 줄이 적용될 때마다 사이에 0이 들어감.

kernel을 4x16 모양의 행렬로 바꾼 것에 이어 input도 모양을 바꾸어보자(4x4에서 16x1로)
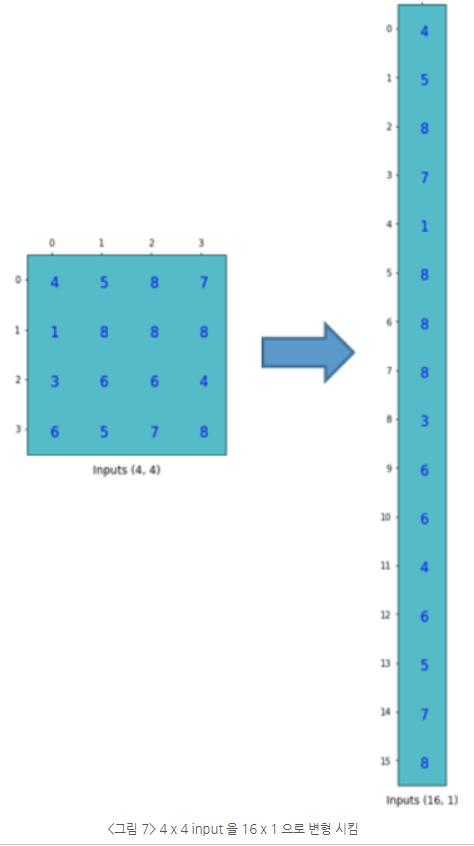
이렇게 바꾼 kernel과 input을 계산하면 어떤 결과가 나오는가?
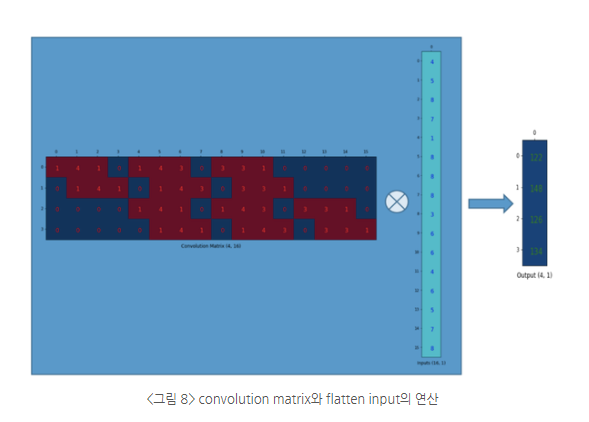
4 x 1 형태의 행렬이 나옴.
즉 현재 2 x 2 라는 output 을 4 x 4 형태로 만들어야 하는데 어떻게 output 1개 값을 input의 9개의 값으로 바꿀 수 있는지 모름.
(2 x 2 output) x (?) = (4 x 4 input) 에서 ?에 들어갈 내용을 모르는 것.
여기에 flatten을 적용하면 (4 x 1 output) x (?) = (16 x 1 input) 이라는 식이 나옴.
그런데 위의 과정들을 통해서 (16 x 1 input) x (4 x 16 convolution matrix) = (4 x 1 output) 이라는 형태를 확인함. 따라서 이 식에서 convolution matrix를 반대쪽으로 이항하면 ?가 무엇인지 알 수 있을 것!
[출처] [Deep learning] Upsampling (Transposed Convolution) 설명|작성자 초밥이다
즐기며 사는 남자 : 네이버 블로그
수처작주 입처개진
blog.naver.com
4.2 전치합성곱
Figure 2.1에 나타난 합성곱의 연결 패턴을 유지하면서 4차원 공간에서 16차원 공간으로 매핑하는 경우를 생각해보기
=> 이 작업을 전치 합성곱이라고 함.
전치 합성곱은 합성곱의 전방향과 역방향 전파를 교환함으로써 작동. 이를 이해하는 한 가지 방법은 커널이 합성곱을 정의하지만 직접적인 합성곱인지 아니면 전치 합성곱인지는 전방향과 역방향 전파가 어떻게 계산되는지에 따라 결정됨.
예를 들어, 커널 w는 전방향 및 역방향 전파가 각각 C와 CT와의 곱셈으로 계산되는 합성곱을 정의하지만, 또한 전치 합성곱을 정의함. 이 전치 합성곱의 전방향 및 역방향 전파는 각각 아래와 같이 계산됨.

직접적인 합성곱으로 전치 합성곱을 흉내 낼 수 있음. 단점은 일반적으로 입력에 많은 열과 행을 추가하는 것을 포함하며, 이로 인해 효율성이 훨씬 떨어지는 구현이 될 수 있다는 점.
4.3 No zero padding, unit strides, transposed(zero 패딩 없음, 단위 스트라이드, 전치합성곱)
전치합성곱을 초기 feature map의 모양을 복원하는 작업으로 간주할 수 있음

Figure 2.1로 보자면, 이 합성곱의 전치는 2x2에 적용될 때 4x4의 출력을 가지게 될 것임.
전치합성곱의 결과를 얻는 또 다른 방법은 동등하지만 훨씬 비효율적인 직접합성곱을 적용하는 것. 이를 설명한 예제는 2x2 입력에 3x3 커널을 적용하여 단위 스트라이드로 패딩된 2x2의 0으로 둘러싸인 영역을 합성하는 것으로 처리할 수 있음(즉, i0 = 2, k0 = k, s0 = 1 및 p0 = 2)

영향을 미치는 패턴을 이해하는 하나의 방법은 전치 합성곱의 연결 패턴을 고려하고 이를 이용하여 동등한 합성곱의 설계를 안내하는 것. 예를 들어, 직접 합성곱의 입력의 왼쪽 위 픽셀은 출력의 왼쪽 위 픽셀에만 영향을 미치고, 오른쪽 위 픽셀은 오른쪽 위 출력 픽셀에만 연결되며, 이와 같은 방식으로 진행됨.
동등한 합성곱에서 동일한 연결 패턴을 유지하려면 입력을 제로 패딩해야 함. 이 때 패딩은 커널의 첫 번째(왼쪽 위) 적용이 왼쪽 위 픽셀만을 포함하도록 해야 함. 즉, 패딩은 커널의 크기에서 1을 뺀 값과 같아야 함. 즉 커널을 왼쪽 위에 적용할 때 input 자료의 맨 왼쪽 위 픽셀만 포함해도록 해야 한다는 것 같은데?

위의 그림과 연결 지으면 o = 2 + (3-1) = 4
4.4 Zero padding, unit strides, transposed(zero 패딩 있음, 단위 스트라이드, 전치합성곱)
패딩되지 않은 합성곱의 전치행렬이 제로 패딩된 입력을 합성하는 것과 동등하다는 사실을 알고 있다면, 제로 패딩된 합성곱의 전치행렬은 더 적은 수의 제로로 패딩된 입력을 합성하는 것으로 추측하는 것이 합리적일 것.

5x5의 input에 4x4의 kernel, 2x2의 제로패딩, stride=1을 적용했던 합성곱(output이 6임)의 전치합성곱 구하기

위의 그림에 적용하면 o = 6 + (4-1) - 2x1 = 7 => 왜 이거지? 실제로 그려보면 output size는 5가 나온다!
4.4.1 Half(same) padding, transposed

5x5 input에 3x3 kernel, half padding(즉 1칸 제로패딩)의 경우 output이 input과 마찬가지로 5x5 사이즈이다.
이 예시의 전치합성곱을 계산하면

o = 5 + (3-1) - 2x1 = 5 따라서 input과 output의 사이즈가 같음.
4.4.2 Full padding, transposed
패딩이 없는 합성곱과 동등한 전치합성곱은 전체 패딩을 포함함.

5x5 input, 3x3 kernel, full padding, unitstride(i=5, k=3, s=1, p=2)의 output size는 7
위의 전치합성곱은 7x7 input, 3x3 kernel, no padding
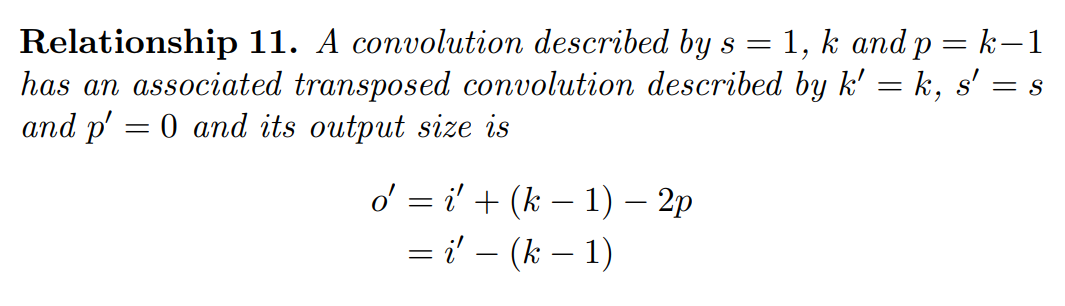
o = 7 + (3-1) - 2x2 = 5. 따라서 output size는 5가 된다.
4.5 No zero padding, non-unit strides, transposed(비단위 스트라이드)
스트라이드가 1보다 큰 합성곱의 전치는 스트라이드가 1보다 작은 동등한 합성곱을 수반함. 이로 인해 전치합성곱이 때때로 분수 스트라이드 합성곱(fractionally strided convolutions)이라고 불림.
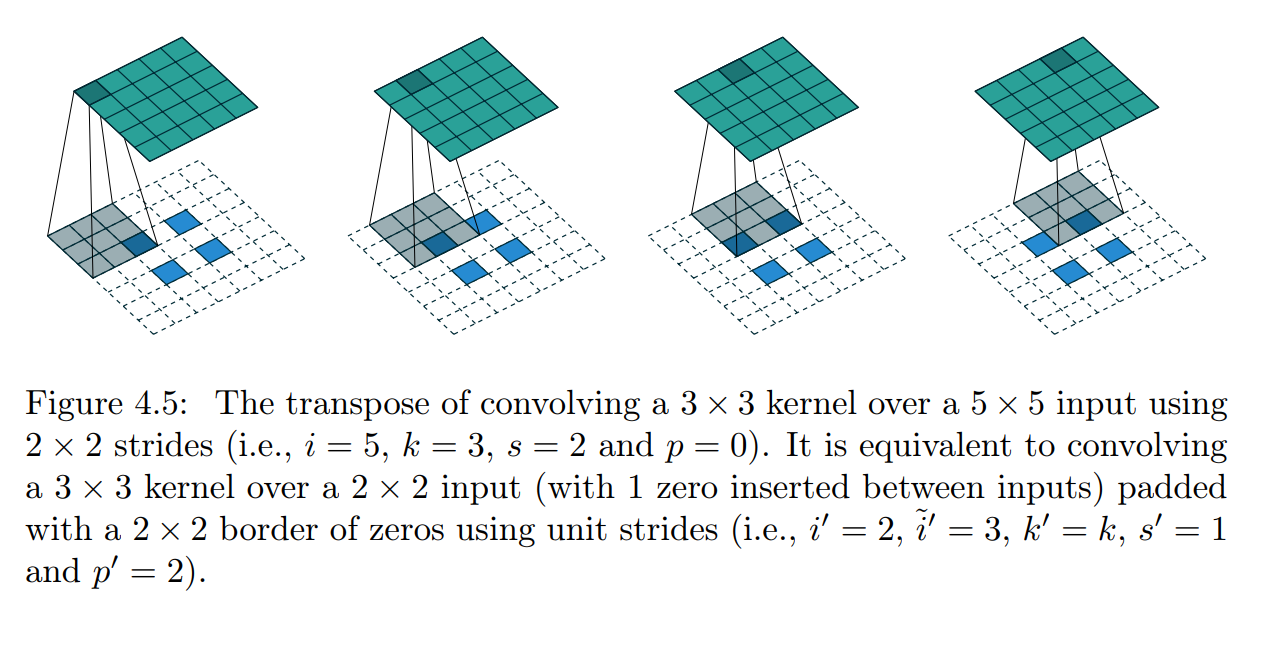
5x5 input, 3x3 kernel, 2x2 stride, padding=0 => output size는 2
Figure 4.5를 보면 입력 단위 사이에 0이 삽입되어 kernel이 unit stride보다 느리게 움직임.
위의 예시를 보면 원래의 합성곱 전치로 2x2 input(사이사이에 0이 삽입됨), 3x3 kernel, 2 padding, unit stride

o = 1(3-1) + 3 = 5 (원래 input size는 2지만 중간에 0이 삽입되어서 input size가 3이 되었음)
4.6 Zero padding, non-unit strides, transposed

input 5x5, kernel 3x3, padding 1x1, stride 2x2 => outputsize 는 3
이에 대한 전치합성곱은 3x3 input(사이에 0 삽입), 3x3 kernel, 1x1 padding, unitstride.

o = 1(5-1) + 3 - 2x1 = 5 => 원래는 input이 3이지만 중간에 0을 끼워넣어서 5가 된다.
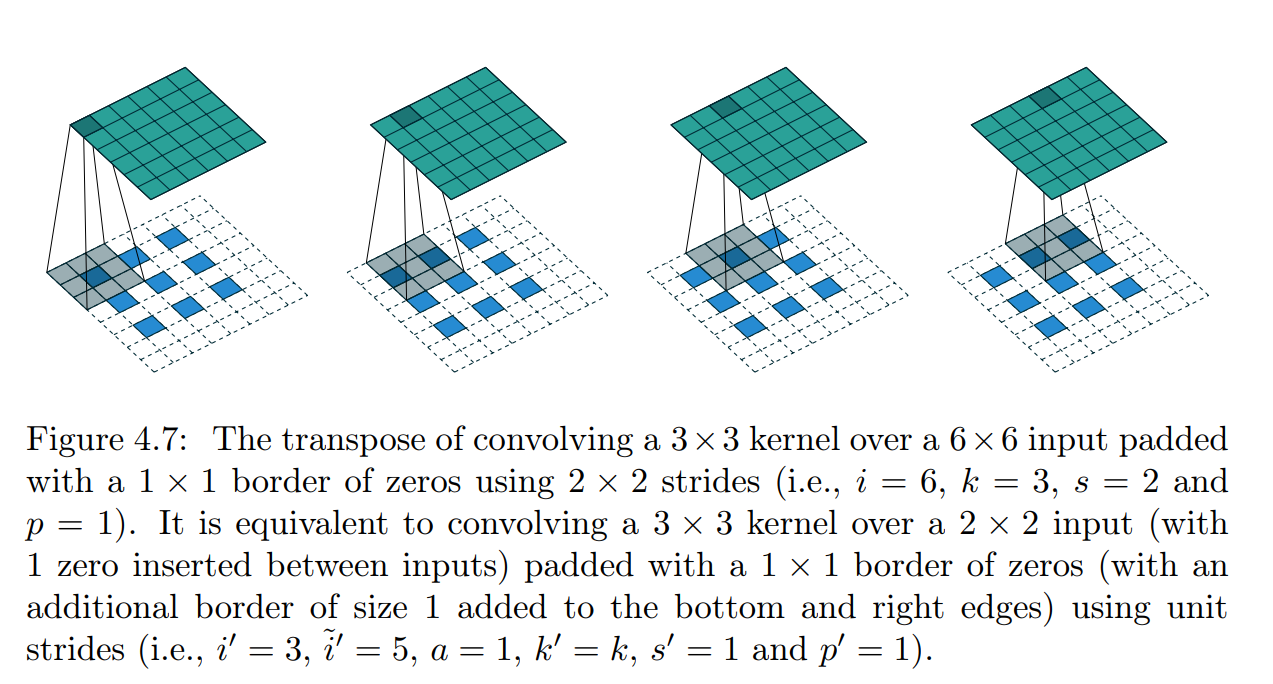
input 6x6, kernel 3x3, padding 1x1, stride 2 => output size = 3x3
이에 대한 전치합성곱은 3x3 input, 3x3 kernel, 1 padding, unit stride
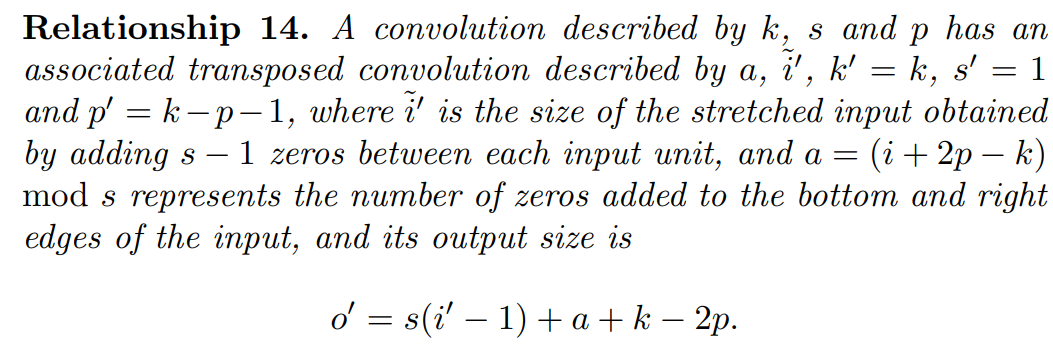
o = 1(5-1) + 1 + 3 - 2x1 = 6 => output size = 6x6
Chapter 5
Miscellaneous convolutions
5.1 Dilated convolutions
확장합성곱 또는 atrous convolutions라고도 알려진 독특한 합성곱. 전통적인 합성곱 커널에 간격이나 구멍을 도입하여 파라미터 수를 늘리지 않고 수용 영역을 늘리는 것을 포함함. 이 기술은 상대적으로 적은 수의 파라미터를 유지하면서 다중 스케일에서 특징을 캡처할 수 있게 해줌.
전통적인 합성곱: 표준 합성곱 연산에서 커널이 입력 데이터 위를 이동하면서 각 위치에서 커널과 해당 입력 부분 간의 원소별 곱셈을 계산. 수용 영역은 커널의 크기에 따라 결정됨
확장 합성곱: 확장 합성곱에서는 커널의 원소 사이에 간격이나 구멍을 추가함. 이 구멍은 커널의 원소 간에 간격을 만들어 내며, 이를 통해 커널은 입력 데이터의 더 넓은 영역에서 정보를 캡처할 수 있음
확장률은 커널의 원소 사이의 간격을 결정함. 확장률 1은 표준 합성곱에 해당하며, 1보다 큰 확장률은 원소 간에 간격을 만듦. 확장률을 조정함으로써 수용 영역과 합성곱으로 캡처되는 특징의 크기를 제어할 수 있음. 또한 확장률은 추가적인 하이퍼파라미터 d로 제어됨. 구현 방법은 다양할 수 있지만 일반적으로 커널 원소 사이에 d-1개의 공간을 삽입함. 따라서 d=1은 일반적인 합성곱을 나타냄.
확장률 d와 출력크기 o 사이의 관계를 이해하기 위해서는 d가 효과적인 커널 크기에 미치는 영향을 생각하는 것이 유용함. 크기 k의 커널을 요인 d로 확장하면 효과적인 크기는 다음과 같음
k = k + (k − 1)(d − 1)

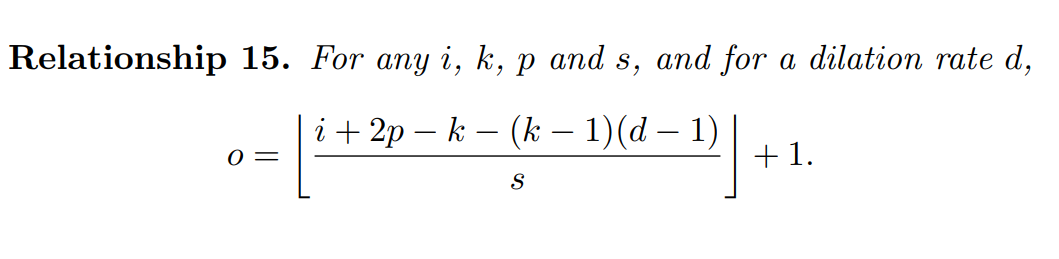
input 7x7, kernel 3x3, d=2, stride=1, padding=0
d-1 = 1 이니까 kernel 원소 사이사이에 간격을 한 개씩만 끼워넣어서 커널의 크기가 5x5가 됨. output은 3x3
o = {7+2*0 - 3 - (3-1)(2-1)} / 1 + 1 = 3
더 큰 커널을 사용하는 대신 커널 원소 사이에 공간을 삽입하여 확장 합성곱을 사용하는 이유
- 수용 영역 증가: 확장 합성곱을 사용하면 파라미터 수를 크게 늘리지 않고 수용 영역을 증가시킬 수 있음. 더 큰 커널은 파라미터 수가 급격히 증가하여 계산 및 메모리 요구 사항이 높아질 수 있음
- 매개변수 효율성: 커널 원소 사이에 공간을 삽입함으로써 실제 커널 크기를 증가시키지 않고도 효과적인 크기를 "확장"할 수 있음. 이는 많은 파라미터를 도입하지 않으면서 더 넓은 문맥에서 특징을 캡처할 수 있다는 의미임.
- 계층적인 특징 학습: 확장 합성곱은 다양한 스케일에서 특징을 캡처하기 위해 스택으로 쌓을 수 있음. 여러 확장률을 사용하여 네트워크는 모델을 지나치게 복잡하게 만들지 않으면서 계층적인 특징을 학습할 수 있음. 더 큰 커널은 특징의 스케일을 동일하게 조절하기 어려울 수 있음.
- 효율적인 병렬화: 확장 합성곱은 병렬 처리에 매우 적합함. 커널 원소 사이의 간격으로 인해 입력의 다른 위치에서 독립적인 계산이 가능해져 더 큰 커널보다 병렬화하기에 적합함.
- 과적합 감소: 더 큰 커널은 많은 매개변수를 지원할 충분한 데이터가 없을 때 과적합을 야기할 수 있음. 확장 합성곱은 매개변수 수의 급증으로 인한 과적합의 위험 없이 효과적인 수용 영역을 확장할 수 있는 방법을 제공.
- 정규화 효과: 확장으로 인해 도입되는 간격은 정규화의 형태로 작용할 수 있음. 이는 모델이 노이즈를 맞추는 것을 방지하고 데이터에서 더 의미 있는 패턴을 캡처하도록 유도할 수 있음.
'CNN' 카테고리의 다른 글
| (개념)합성곱 신경망(Convolutional Neural Network: CNN)의 구조 (0) | 2023.07.12 |
|---|