2024. 9. 6. 20:37ㆍ알고리즘
♠ BFS(Breadth-First-Search) 의 개념
그래프 탐색
하나의 정점(노드)로부터 시작하여 차례대로 모든 노드를 한 번씩 방문하는 것. BFS도 그래프 탐색 방법 중 하나이다.
BFS는 루트 노드(혹은 다른 임의의 노드)에서 시작하여 인접한 노드를 먼저 탐색하는 방법이다. 따라서 시작 노드로부터 가까운 노드를 먼저 방문하고, 멀리 떨어져있는 노드를 나중에 방문하는 순회 방법이다.

♠ BFS의 특징
- BFS는 시작 노드에서 목표 노드까지의 최단 경로를 구하는 데 유용하다. 시작 노드로부터 가까운 노드부터 탐색하기 때문이다. DFS의 경우, 이와 달리 깊이를 끝까지 탐색한 후 옆으로 이동하기 때문에 최단 경로를 구하기 어렵다.
- BFS를 구현할 때는 노드 방문 여부를 검사해야 한다. 방문 여부를 제대로 검사하지 않으면 무한 루프에 빠질 수 있다.
- 방문한 노드들을 차례로 저장한 후 꺼낼 수 있는 자료 구조인 큐(queue)를 사용한다. 즉 선입선출(FIFO) 원칙으로 노드들을 탐색한다. 그래프 탐색은 큐 안에 노드가 모두 없어질 때까지 진행한다.
♠ BFS 기본 코드
def bfs(start):
q = queue.Queue()
visited = [False]*(n+1)
q.put([start])
visited[start] = True
while q:
node = q.get()
for i in graph[node]:
if not visited[i]:
visited[node] = True
q.put(node)♠ BFS 알고리즘 문제 풀기
백준 알고리즘 11725번(https://www.acmicpc.net/problem/11725)

import sys
input = lambda: sys.stdin.readline().rstrip()
import queue
n = int(input())
graph = [[] for _ in range(n+1)]
#그래프 만들기
for i in range(n-1):
a, b = map(int, input().split())
graph[a].append(b)
graph[b].append(a)
print(graph)
# graph: 그래프, start: 시작 노드, visited: 방문 여부 확인
def bfs(start):
visited = [False]*(n+1)
q = queue.Queue()
q.put(start)
visited[start] = True
#부모 노드를 저장할 리스트
parents = [0]*(n+1)
while q:
node = q.get()
for neighbor in graph[node]:
if not visited[neighbor]:
visited[neighbor] = True
parents[neighbor] = node
q.put(neighbor)
return parents
answer = bfs(1)
for i in range(2, n+1):
print(answer[i])
import sys
input = lambda: sys.stdin.readline().rstrip()
from collections import deque
n = int(input())
graph = [[] for _ in range(n+1)]
#그래프 만들기
for i in range(n-1):
a, b = map(int, input().split())
graph[a].append(b)
graph[b].append(a)
print(graph)
# graph: 그래프, start: 시작 노드, visited: 방문 여부 확인
def bfs(start):
visited = [False]*(n+1)
que = deque([start])
visited[start] = True
#부모 노드를 저장할 리스트
parents = [0]*(n+1)
while que:
node = que.popleft()
for neighbor in graph[node]:
if not visited[neighbor]:
visited[neighbor] = True
parents[neighbor] = node
que.append(neighbor)
print(que)
return parents
answer = bfs(1)
for i in range(2, n+1):
print(answer[i])
탐색 과정 출력


루트 노드 1부터 시작하여 너비우선탐색을 한다. 그런데 queue의 구조를 사용했을 때는 시간 초과가 났다. 반면, deque 구조를 사용했을 때는 시간 초과가 나지 않았다. deque는 스텍과 큐의 기능을 모두 가진 객체로, 출입구를 양쪽에 가지고 있는데 deque가 Queue 클래스보다 시간복잡도가 훨씬 작다고 한다. 파이썬에서는 deque가 훨씬 효율적으로 동작한다.
♠ DFS(Depth-First-Search)의 개념
DFS 역시 그래프 탐색 기법 중 하나로, 시작 노드에서 깊이를 우선으로 자식 노드들을 탐색하는 방법이다. 미로 찾기를 할 때 막다른 길이 나올 때까지 계속 가다가 더 이상 갈 수 없게 되면 가장 가까운 갈림길로 돌아와서 다른 갈림길로 들어가는 것과 비슷하다.
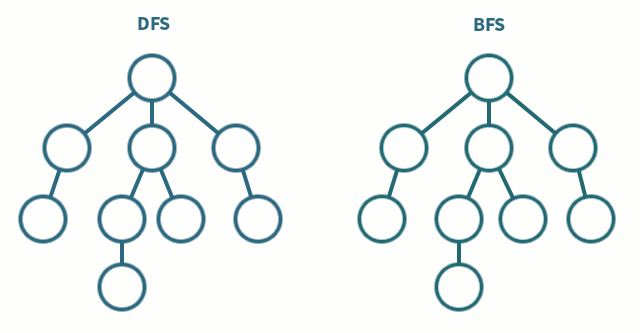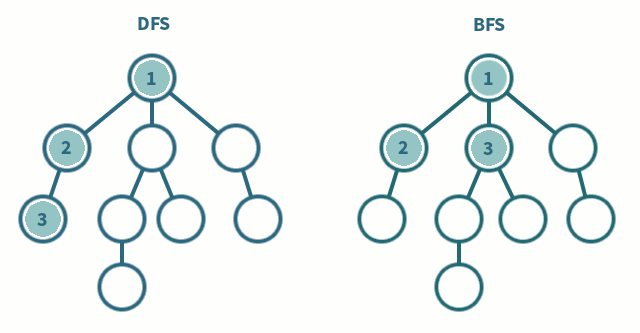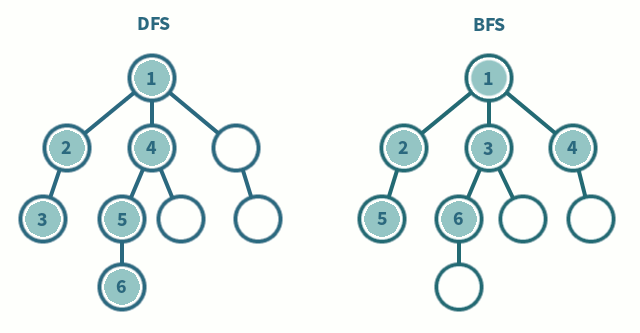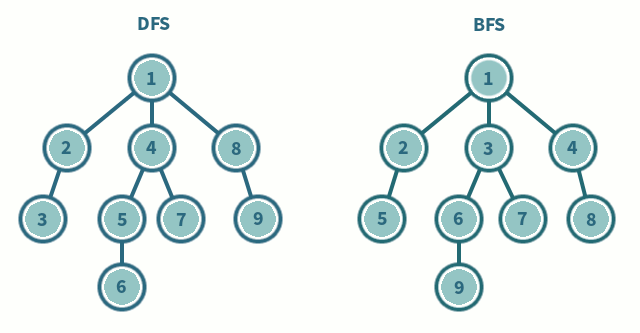
♠ DFS의 특징
- 목표가 특정한 노드, 또는 모든 노드에 최대한 빨리 도달하는 문제일 때 유용하다.
- 두 노드 사이의 최단 경로를 찾으려는 경우, 사용하기 좋은 알고리즘이 아닐 수 있다.
- 반복문이나 재귀문을 활용하여 구현한다.
♠ DFS 기본 코드
def dfs(start):
que.append(start)
visited[start] = True
for node in graph[start]:
if not visited[node]:
dfs(node)
parents[node] = start
return parents
♠ DFS 알고리즘 문제 풀기
import sys
input = lambda: sys.stdin.readline().rstrip()
sys.setrecursionlimit(1000000)
from collections import deque
n = int(input())
graph = [[] for _ in range(n+1)]
#그래프 만들기
for i in range(n-1):
a, b = map(int, input().split())
graph[a].append(b)
graph[b].append(a)
que = deque([])
visited = [False]*(n+1)
parents = [0]*(n+1)
def dfs(start):
que.append(start)
visited[start] = True
print(que, visited)
for node in graph[start]:
if not visited[node]:
dfs(node)
parents[node] = start
return parents
answer = dfs(1)
for i in range(2, n+1):
print(answer[i])
탐색 과정 출력
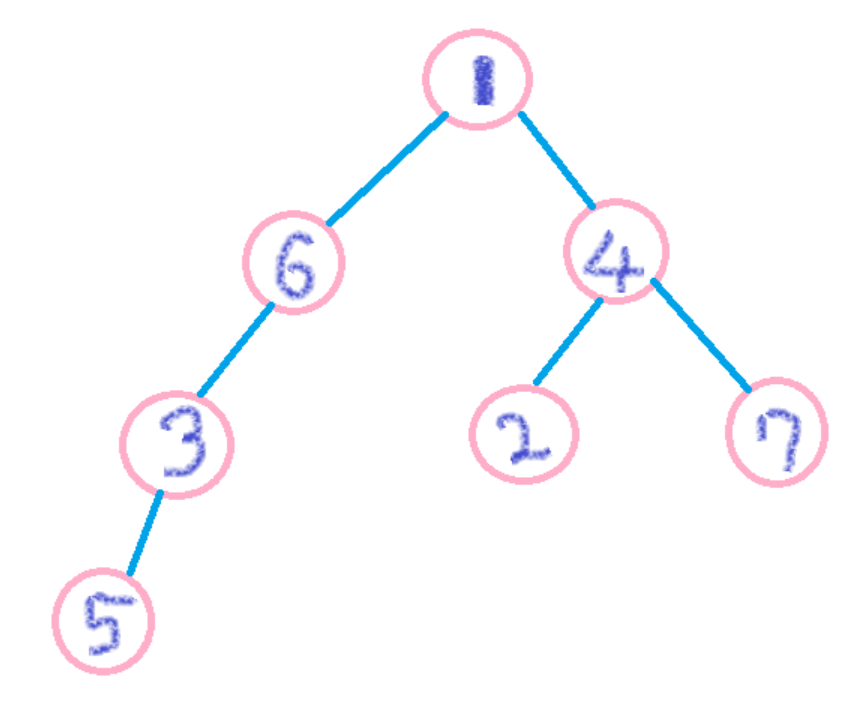

재귀함수를 사용했을 때 recursion error가 발생한다면 stack을 사용하여 DFS를 실행할 수도 있다.
import sys
input = lambda: sys.stdin.readline().rstrip()
n = int(input())
graph = [[] for _ in range(n+1)]
#그래프 만들기
for i in range(n-1):
a, b = map(int, input().split())
graph[a].append(b)
graph[b].append(a)
#stack 사용하기
visited = [False]*(n+1)
parents = [0]*(n+1)
def dfs(start):
stack = [start]
visited[start] = True
while stack:
node = stack.pop()
for neighbor in graph[node]:
if not visited[neighbor]:
visited[neighbor] = True
parents[neighbor] = node
stack.append(neighbor)
print(stack)
return parents
answer = dfs(1)
for i in range(2, n+1):
print(answer[i])
탐색 과정 출력


♣ 참고 자료
ABOUT BFS
[알고리즘] 너비 우선 탐색 (BFS, Breadth-First Search)이란?
너비 우선 탐색 (BFS, Breadth-First Search) - 그래프에서 가까운 노드부터 우선적으로 탐색하는 알고리즘 - 큐 자료구조를 이용함 장점 - 출발노드에서 목표노드까지의 최단 길이 경로를 보장한다. 단
seokii.tistory.com
https://baechu-story.tistory.com/29
[파이썬 알고리즘] DFS와 BFS를 이용한 그래프 탐색
1. 그래프란? 연결된 객체 간의 관계를 표현하는 자료구조 그래프 G(V, E)는 어떤 자료나 개념을 포함하는 정점의 집합 V(vertex)와 이를 연결하는 간선의 집합 E(edge)로 구성된다. 정점(node, vertex): 여
baechu-story.tistory.com
ABOUT DFS
https://olrlobt.tistory.com/35
[알고리즘] DFS (Depth-First Search) : 깊이 우선 탐색 알고리즘이란?
깊이 우선 탐색(DFS, Depth-First Search) 트리나 그래프를 탐색하는 기법 중 하나로, 시작 노드에서 자식의 노드들을 순서대로 탐색하면서 깊이를 우선으로 탐색하는 알고리즘이다. 깊이를 우선시하
olrlobt.tistory.com
[알고리즘 : 그래프 이론] 그림으로 쉽게 보는 DFS 기본, 개념, 설명, 코드
DFS(Depth First Search : 깊이 우선 탐색) 그래프, 어렵습니다. 그래프에 대한 이론은 많은 걸로 알고 있습니다. 그중에서 대표적인 것이 바로 탐색 기법인데요. DFS와 BFS라는 녀석, 이 둘이 가장 대표적
reakwon.tistory.com
https://chaeyami.tistory.com/184
[백준] 11725번 : 트리의 부모 찾기 (DFS/BFS 실버Ⅱ) - Python, Java
문제 https://www.acmicpc.net/problem/11725 11725번: 트리의 부모 찾기 루트 없는 트리가 주어진다. 이때, 트리의 루트를 1이라고 정했을 때, 각 노드의 부모를 구하는 프로그램을 작성하시오. www.acmicpc.net
chaeyami.tistory.com
'알고리즘' 카테고리의 다른 글
| 세그먼트 트리 (0) | 2024.10.22 |
|---|---|
| 데이크스트라 vs 플로이드-워셜 (0) | 2024.09.07 |
| 슬라이딩 윈도우(백준 알고리즘 12847번) (0) | 2024.09.05 |
| 플로이드 워셜 알고리즘(Floyd Warshall Algorithm, 백준 알고리즘 2458번) (0) | 2024.08.21 |
| 데이크스트라 알고리즘(백준 알고리즘 13549번) (0) | 2024.08.12 |