2024. 8. 21. 09:58ㆍ알고리즘
♣ 플로이드 워셜 알고리즘
데이크스트라 알고리즘이 한 지점에서 다른 지점까지의 최단 경로를 구하는 알고리즘이라면 플로이드 워셜 알고리즘은 모든 지점에서 다른 모든 지점까지의 최단 경로를 모두 구하는 알고리즘이다.
플로이드 워셜은 모든 지점에서 다른 모든 지점까지의 최단 거리를 저장하기 때문에 2차원 테이블에 최단 거리 정보를 저장한다. 또한 플로이드 워셜은 DP 알고리즘에 속한다.
[단계별 설명]
1단계. 그래프의 노드와 간선에 따라 최단 거리 테이블을 갱신한다. (노드 사이에 간선이 없는 경우는 무한으로 설정)

2단계. 1번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다.

예를 들면 1단계에서는 노드 3에서 노드 2으로 가는 기본 경로가 없어서 거리가 무한이었으나 1번 노드를 거쳐가게 되면 3 -> 1 -> 2 로 최단거리가 9가 된다. 9는 무한보다 작기 때문에 D32를 9로 갱신한다. 점화식으로 따지면 아래와 같다.
D32 = min(D32, D31+D12)
3단계: 2번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다.

1번 노드에서 3번 노드로 가는 간선이 없어서 2단계까지 1-3 은 무한이었으나 2번 노드를 거쳐서 1 -> 2 -> 3 으로 이동하면 최단 거리가 4+7=11 이 된다. 점화식으로 따지면 아래와 같다.
D13 = min(D13, D12+D23)
이렇게 각각의 노드를 거쳐서 가는 경우를 고려하여 테이블을 갱신한다.
♣ 백준 알고리즘 2458번 이해 및 해결 방법




학생들의 키를 노드처럼 그래프를 만들어 비교하는 문제이다. 예제 입력을 이용하여 학생들의 키를 비교한 결과를 최대한 연결하면 아래와 같다.

위 그래프에서 자신의 키가 몇 번째로 큰지 알 수 있는 노드는 모든 다른 노드들과 연결될 수 있는 4뿐이다. (1, 3, 5 보다는 키가 크고, 2, 6보다는 키가 작음) 다른 노드들은 모든 다른 노드들과 연결된 건 아니기 때문에 비교가 불가능하다. 예를 들어 노드 3을 보자면 2, 4, 6보다는 키가 작지만 1, 5보다 키가 작은지, 큰지는 알 수 없다.
이를 플로이드-워셜 알고리즘을 사용하여 표를 그리면 아래와 같다. 각 노드 사이의 간선거리는 1로 설정했다.
1단계. 그래프의 노드와 간선에 따라 최단 거리 테이블을 갱신한다. (노드 사이에 간선이 없는 경우는 무한으로 설정)
 |
 |
2단계. 1번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다.
위의 그래프를 보면 도착 노드를 1번 노드로 하는 노드들이 없기 때문에 2단계에는 갱신할 내용이 없다.
3단계. 2번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다.
그래프를 보면 2번 노드를 거쳐서 갈 수 있는 노드들이 없기 때문에 3단계에는 갱신할 내용이 없다.
4단계. 3번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다.
그래프를 보면 도착노드를 3번 노드로 하는 노드들이 없기 때문에 4단계에는 갱신할 내용이 없다.
5단계. 4번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다.
 |
 |
노드 4를 거쳐서 갈 수 있는 경로는 D56, D52, D32, D36 이 있다. 점화식은 아래와 같다.
D56 = min(D56, D54+D46)
D52 = min(D52, D54+D42)
D32 = min(D32, D34+D42)
D36 = min(D36, D34+D46)
6단계. 5번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다.
 |
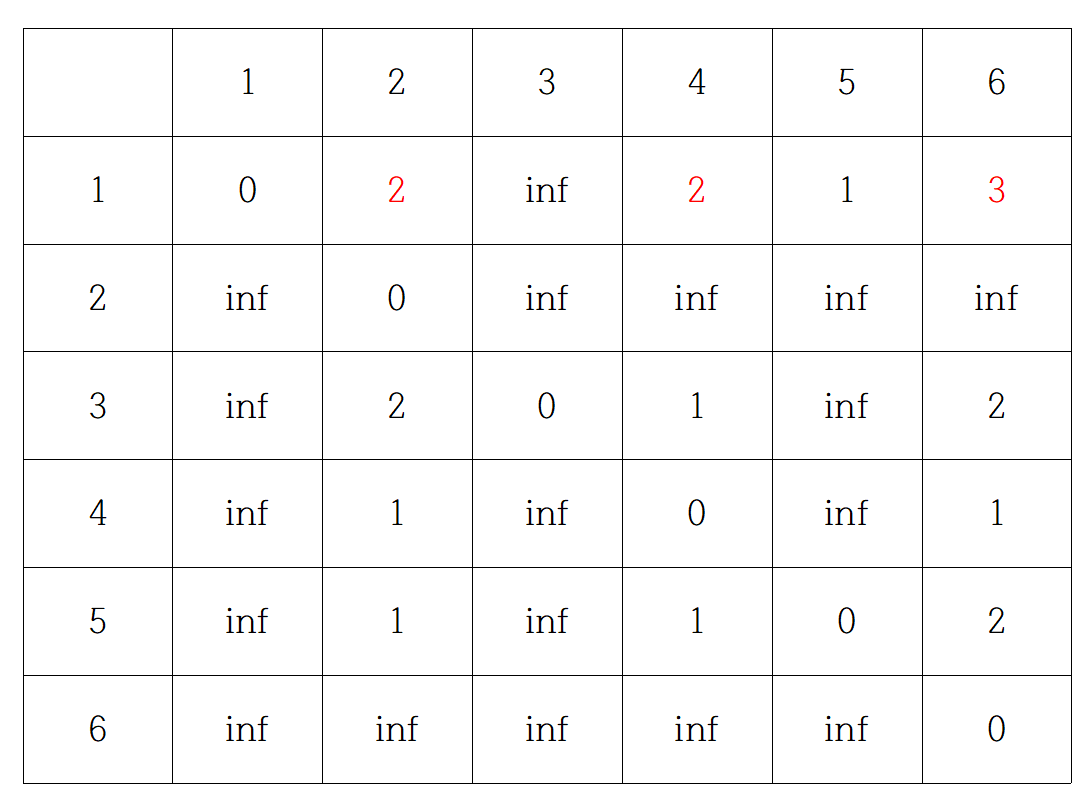 |
노드 5를 거쳐서 갈 수 있는 경로는 D14, D12, D16이 있다. 점화식은 아래와 같다.
D14 = min(D14, D15+D54)
D12 = min(D12, D15+D52)
D16 = min(D16, D15+D56)
7단계. 6번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다.
6번 노드를 거쳐서 갈 수 있는 노드들이 없기 때문에 갱신할 내용이 없다.
♣ 백준 알고리즘 2458번 코드
import sys
input = lambda: sys.stdin.readline().rstrip()
n, m = map(int, input().split())
#2차원 그래프 만들기
inf = 1e9
graph = [[inf]*(n+1) for _ in range(n+1)]
#자기 자신으로 가는 간선은 0으로 만들기
for i in range(1, n+1):
for j in range(1, n+1):
if i == j:
graph[i][j] = 0
#간선에 대한 정보를 받아서 테이블 갱신
for i in range(m):
a, b = map(int, input().split())
graph[a][b] = 1
total = [0]*(n+1)
# 각 노드를 거치면서 테이블 갱신
for k in range(1, n+1):
for a in range(1, n+1):
for b in range(1, n+1):
graph[a][b] = min(graph[a][b], graph[a][k]+graph[k][b])
for a in range(1, n+1):
for b in range(1, n+1):
if graph[a][b] != inf and a!=b:
total[a] += 1
total[b] += 1
# print(a, b, total)
print(total.count(n-1))
♣ 참고
플로이드 워셜 알고리즘
[알고리즘] 플로이드 워셜 알고리즘 (Floyd-Warshall Algorithm)
지난 포스팅에서는 다익스트라 알고리즘에 대해 작성했었다. 다익스트라의 경우 한 지점에서 다른 특정 지점까지의 최단 경로를 구하는 알고리즘이다. 그러나 모든 지점에서 다른 모든 지점까
velog.io
https://banwolcode.tistory.com/33
플로이드-워셜 알고리즘 (Floyd-Warshall)
플로이드-워셜 알고리즘 다익스트라가 하나의 정점에서 모든 정점까지의 최단 거리를 구하는 알고리즘이라면 플로이드-워셜 알고리즘은 모든 노드 간의 최단 경로를 구하는 알고리즘이다. 그
banwolcode.tistory.com
'알고리즘' 카테고리의 다른 글
| BFS(너비우선탐색) vs DFS(깊이우선탐색) (0) | 2024.09.06 |
|---|---|
| 슬라이딩 윈도우(백준 알고리즘 12847번) (0) | 2024.09.05 |
| 데이크스트라 알고리즘(백준 알고리즘 13549번) (0) | 2024.08.12 |
| 유니온 파인드/분리집합 알고리즘(백준알고리즘 1043번) (0) | 2024.07.25 |
| CCW(백준 알고리즘 17386, 17387번) (0) | 2024.07.11 |