2023. 7. 16. 13:33ㆍ딥러닝 모델: 파이토치
♣ 최적화(옵티마이저)
손실함수 값을 최소화하는 파라미터를 구하는 과정
즉 모델이 예측한 값과 실제값의 차이를 최소화하는 신경망 구조의 파라미터를 찾는 과정
손실함수 값의 변화에 따라 가중치(weight)나 편향(bias)을 업데이트함
딥러닝에서는 최적의 파라미터(가중치)를 찾기 위해 가장 기본이 되는 알고리즘으로 경사하강법(Gradient Descent)를 사용함.
♣경사하강법(Gradient Descent)
손실 함수 그래프에서 값이 가장 낮은 지점으로(손실 함수의 최솟값이 되는 방향으로) 경사를 타고 하강하는 기법
수행 과정
- 어느 지점에서든지 시작한다(initial guesses에서)
- cost를 줄이는 방향으로 W와 b를 조금씩 바꿈
- parameter(W와 b)를 바꿀 때마다 경사도 계산
- 위의 과정 반복
경사하강법의 한계
- Local Minimum에 빠질 수 있음
- Saddle point를 벗어나지 못함
Local Mimimum(그래프 내 일부만 고려했을 때의 최솟값)
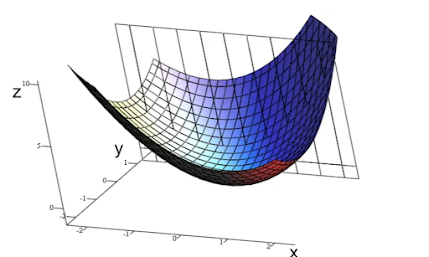
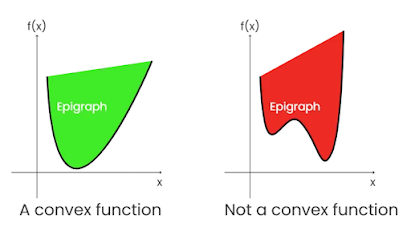
경사하강법이 잘 작동하려면 함수가 convexfunction(볼록함수)여야 함. 비볼록함수(Non-convex function)의 경우, 파라미터의 초기 시작 위치에 따라 최적의 값이 달라짐.
위의 그림처럼 아래 또는 위로 볼록한 함수를 볼록함수라고 함. 볼록함수는 초기 파라미터 값이 어떻게 설정되어도 경사하강법을 이용하면 최적의 값에 도달함.
하지만 비블록함수의 경우, 경사하강법 사용 시 파라미터 값의 시작 위치에 따라 최적의 값이 달라짐. 가장 낮은 값으로 이동하는 것이 아니라 부분적으로 낮은 값(local minimum)에 빠질 수 있음. 또한 최적의 값이라고 판단한 값이 Global minimum(목표함수 그래프 전체를 고려했을 때의 최솟값)인지 Local minimum인지 구분하는 것이 불가능함.

Saddle Point
아래 그림의 검은색 점이 안장점임. 안장점은 기울기가 0이지만 최솟값은 아닌 지점을 의미함. A-B 경사에서 보면 안장점이 최솟값이지만 C-D 경사에서 보면 안장점은 최댓값임. 따라서 해당 지점은 미분이 0이지만 조건을 만족하지 않음. 그럼에도 불구하고 경사하강법은 미분이 0일 경우 더 이상 파라미터를 업데이트하지 않기 때문에 안장점을 벗어나지 못함.

※ 참고 자료
1. 최적화: https://heytech.tistory.com/380
[Deep Learning] 최적화 개념과 경사 하강법(Gradient Descent)
📚 목차 1. 최적화 개념 2. 기울기 개념 3. 경사 하강법 개념 4. 경사 하강법의 한계 1. 최적화 개념 딥러닝 분야에서 최적화(Optimization)란 손실 함수(Loss Function) 값을 최소화하는 파라미터를 구하는
heytech.tistory.com
2. 딥러닝 관련 용어: https://www.infoking.site/10
딥러닝 관련 용어(1/2) - 활성화 함수, 옵티마이저
워드투벡을 적용하여 RNN모델을 적용하기 전에, 딥러닝 학습시 필요한 용어들을 한 번 정리하고 넘어가려고 한다. 1. 활성화 함수(Activation Function) 신경망의 뉴런들을 선형 결합한 하면, 선형 모형
www.infoking.site
3. 경사하강법: https://www.blogger.com/blog/post/edit/1173174647759940254/7124967409682667188
Blogger
이메일 또는 휴대전화
accounts.google.com
'딥러닝 모델: 파이토치' 카테고리의 다른 글
| 파이토치 튜토리얼 (1) | 2023.10.07 |
|---|---|
| 밑바닥부터 Learner 클래스 만들기 (0) | 2023.09.20 |
| DataBlock와 DataLoader 비교 (0) | 2023.09.17 |
| ImageDataLoaders vs ImageDataBunch (0) | 2023.08.15 |
| 텐서(Tensor) (0) | 2023.08.07 |