2023. 7. 18. 16:48ㆍResNet
CNN은 망이 깊어질수록 정확도가 향상된다는 것이 일반적인 견해이지만 Gardient Vanishing Problem, 연산량의 과도한 증가 등의 걸림돌 때문에 오히려 망이 깊어질수록 성능이 떨어지는 모습을 보임. ResNet은 Output에 간단한 수정을 가해 Degradation 문제를 완화하고 100장의 레이어가 넘는 네트워크도 학습이 가능하게 만듦.
♣ 14.1 완전합성곱신경망

splitter = GrandparentSplitter(valid_name='val')
데이터를 학습 세트와 검증 세트로 분할하는 방법을 지정하는 부분.
GrandparentSplitter는 주어진 데이터셋의 경로 구조를 기반으로 데이터를 분할하는 방법 중 하나임. valid_name은 검증 세트의 이름을 지정하는 매개변수임. 이 경우 'val'로 설정되어 있으므로, 검증 세트는 'val'이라는 이름의 폴더에서 가져온 데이터로 구성함.
item_tfms=Resize(presize)
데이터셋의 각 항목(item)에 대해 이미지 크기를 조정하는 변환을 적용하는 부분
여기서는 presize는 이용했는데 이는 크기를 조정하기 이전 크기를 나타냄. presize는 학습 이전에 이미지를 사전 조정할 때 사용됨. 따라서 데이터셋의 각 이미지 항목을 이전 크기 presize로 조정하는 변환을 적용한다는 의미. 이를 통해 데이터셋의 모든 이미지가 동일한 크기로 조정되며 모델 학습을 위해 일관된 입력 크기를 제공 가능
batch_tfms=[*aug_transforms(min_scale=0.5, size=resize), Normalize.from_stats(*imagenet_stats)]
미니배치 데이터에 적용되는 변환을 정의하는 부분. aug_transforms는 데이터 증강(augmentation)을 수행하는 변환들을 포함하는 함수. min_scale=0.5는 이미지를 최소 0.5배로 축소하는 변환. 즉 데이터 증강을 통해 이미지에 다양한 변형을 적용하고 크기를 조정하여 모델을 학습시킴.
Normalize.from_stats(*imagenet_stats)
이미지를 정규화하는 변환. Normalize의 from_stats 메서드는 데이터셋의 평균과 표준 편차를 인자로 받아 이러한 통계 정보를 기반으로 데이터를 정규화함. imagenet_stats는 이미지넷(ImageNet) 데이터셋에서 계산된 평균과 표준편차를 의미함. 이를 사용하여 이미지의 픽셀값을 평균과 표준편차로 정규화함. 정규화는 입력 데이터의 스케일을 일치시키고 모델의 학습을 안정화하는 데 도움을 줌.
따라서 미니배치 데이터에 데이터 증강과 정규화를 포함하는 변환을 적용한다는 의미임. 이를 통해 학습 데이터의 다양성을 높이고 입력 데이터를 일관되게 처리하여 모델의 성능 향상을 도모할 수 있음.
item_tfms VS batch_tfms
'item_tfms(항목 변환)'와 'batch_tfms(배치 변환)'의 차이는 데이터 처리 단위에 있음.
- item_tfms(항목 변환):
- 개별 데이터 항목에 적용되는 변환.
- 데이터셋의 개별 항목 (예: 이미지)에 대해 수행되는 전처리 및 증강 작업을 포함
- 데이터셋에서 가져온 각 항목은 개별적으로 변환되어 모델에 입력으로 제공
- batch_tfms(배치 변환):
- 배치 단위로 적용되는 변환
- 데이터 로더가 가져오는 데이터 항목들을 배치로 묶어서(batch) 전체 배치에 대해 적용되는 변환
- 여러 항목을 묶은 배치 단위로 데이터 변환을 수행하므로 처리 속도를 향상시키는 데 도움이 됨
따라서, item_tfms는 데이터셋의 각 항목에 적용되는 개별 변환이고, batch_tfms는 데이터 로더가 가져온 배치 데이터에 대해 한꺼번에 적용되는 변환이라는 점에서 차이가 있음
완전 합성곱 신경망의 구성 및 코드

Convolutional Neural Network(CNN)에서 일반적으로 사용되는 풀링 연산 중 하나로, 입력 데이터를 작은 영역으로 나누고 각 영역의 평균 값을 구하는 연산을 수행함. 평균 풀링 함수의 역할은 입력 x를 높이와 너비 축에서 평균을 계산하여 채널 축만 남긴 3차원 텐서로 만드는 것임. x.mean(2, 3)는 x의 4차원 텐서(batch_size, channels, height, width)에서 2번째 축(높이)과 3번째 축(너비)을 따라 평균을 구한다는 것을 의미함. 이렇게 하면 각 채널별로 높이와 너비에 대한 평균 값을 구하게 됨. 이렇게 구해진 텐서는 이미지의 공간 정보를 간소화시키면서 채널별로 중요한 정보를 유지함.
- 축(axis) 0: 배치 크기 (Batch Size)
- 축(axis) 1: 채널 수 (Number of Channels)
- 축(axis) 2: 높이 (Height)
- 축(axis) 3: 너비 (Width)
함수의 이름은 avg_pool이며, 인자로 x를 받습니다. x는 4차원 텐서로 가정합니다. 4차원 텐서는 배치 크기, 채널 수, 높이, 너비의 차원을 가짐. x가 (batch_size, channels, height, width)와 같은 이미지 텐서를 나타낸다면 x.mean((2, 3))를 호출했을 때 높이와 너비의 차원을 따라 평균을 계산함. 이 연산은 각 이미지의 공간적 차원(x라벨, y라벨)을 각 채널 당 하나의 값으로 축소함.
완전합성곱신경망은 수많은 합성곱 계층 + 단위 축을 제거하는 평탄화 계층 + 최종 선형 계층으로 구성됨
이때 합성곱 계층 중 일부는 스트라이드2로 설정되며 마지막 합성곱 계층 다음에 적응 평균 풀링 계층이 적용됨.
완전합성곱신경망은 물체의 크기나 방향이 여러 개일 때 매우 적합함(대부분의 일반적인 사진)

- nn.Sequential
여러 계층을 순차적으로 연결함
- ConvLayer
CNN에서 학습했던 conv의 모든 기능을 포함한 fastai의 ConvLayer를 활용
컨볼루션 레이어(Convolutional Layer)를 나타내는 fastai 라이브러리의 클래스
ConvLayer의 구성
- 컨볼루션 레이어: ConvLayer의 핵심 구성 요소. 입력 데이터에 대해 컨볼루션 연산을 수행하며 학습 가능한 필터(또는 커널) 세트를 사용. 이러한 필터는 입력 데이터에서 다양한 특징을 감지.
- ReLU 활성화 함수: 컨볼루션 레이어의 출력에 요소별로 ReLU(렉티파이드 리니어 활성화 함수)를 적용. 이를 통해 모델에 비선형성을 도입하며 더 복잡하고 표현력 있는 특징을 학습할 수 있음
- 정규화 유형 (선택 사항): norm_type 매개변수를 사용하여 컨볼루션 연산 후 적용할 정규화 유형을 지정할 수 있습니다. 'batch', 'group', 'instance' 등과 같은 값을 설정할 수 있음.
ConvLayer 사용 예시
ConvLayer(
ni,
nf,
ks = 3,
stride = 1,
padding = NULL,
bias = NULL,
ndim = 2,
norm_type = 1,
bn_1st = TRUE,
act_cls = nn()$ReLU,
transpose = FALSE,
init = "auto",
xtra = NULL,
bias_std = 0.01,
dilation = 1,
groups = 1,
padding_mode = "zeros"
)Arguments
| ni | number of inputs |
| nf | outputs/ number of features |
| ks | kernel size |
| stride | stride |
| padding | padding |
| bias | bias |
| ndim | dimension number |
| norm_type | normalization type |
| bn_1st | batch normalization 1st |
| act_cls | activation |
| transpose | transpose |
| init | initializer |
| xtra | xtra |
| bias_std | bias standard deviation |
| dilation | specify the dilation rate to use for dilated convolution |
| groups | groups size |
| padding_mode | padding mode, e.g 'zeros' |
합성곱 계층을 다 쌓으면 batch_size * ch * h * w(배치 크기, 특정 채널 수, 높이, 너비) 크기의 활성을 얻게 됨
그리고 이를 batch_size * ch 크기의 텐서로 변환해야 함. 따라서 마지막 두 차원에서 h와 w의 평균을 구해서 h와 w를 없애고(위의 avg_pool 함수에서 했듯이, 여기서는 AdaptiveAvgPool2d에서 수행) 이전 모델에서 했듯이 남은 1*1 차원을 기준으로 평평하게 만듦(Flattne에서 수행).
- nn.AdaptiveAvgPool2d(1)
(CNN)에서 사용되는 풀링 연산 중 하나로, 입력 이미지의 크기를 유지하면서 채널별로 평균 값을 계산하는 연산임. 위에서 설명한 avg_pool을 대신하는 파이토치 모듈임. 이는 입력 이미지의 크기가 다양하거나 고정되어 있더라도 일정한 크기의 출력을 얻을 수 있게 해줌.
일반적인 풀링 연산은 사전에 지정된 풀링 크기를 기준으로 입력 이미지를 격자로 분할하고, 각 격자 내의 값을 다양한 방식으로 집계하여 출력을 생성함. 이러한 경우, 입력 이미지의 크기가 변하면 풀링 연산의 결과도 변할 수 있음.
반면에 Adaptive Average Pooling은 출력의 크기를 미리 지정하는 대신, 출력의 크기를 입력 이미지의 크기에 따라 자동으로 조절합니다. 입력 이미지의 크기가 크거나 작아지더라도 항상 일정한 크기의 출력(batch_size, channles, 1, 1)을 얻을 수 있음. 이를 통해 입력 이미지의 공간적인 정보를 요약하고 모델이 임의의 크기의 입력을 처리할 수 있도록 함.
- Flatten()
Flatten() 계층은 공간적인 차원을 제거하고 출력을 평탄화하여, (배치 크기, 채널 수) 형태의 2D 텐서를 생성하는 계층.
- nn.Linear(256, dls.c)
입력 크기가 256이고 출력 크기가 dls.c인 선형 계층을 추가함. 이 선형 계층은 모델의 최종 출력을 생성함. 여기서 dls.c는 데이터로더(dataloaders)에서 클래스 수를 나타내며, 분류 작업에서 각 클래스에 대한 확률 값을 출력함.
- nn.AdaptiveAvgPool2d(1) VS Flatten()
- AdaptiveAvgPool2d(1):
- AdaptiveAvgPool2d(1)은 공간적 다운샘플링을 수행하여 입력 텐서의 공간적 차원을 축소하고 동시에 채널 정보를 보존하는 풀링 연산입니다.
- 공간적 차원(예: 높이와 너비)을 가진 텐서를 입력으로 받아 1x1 크기의 고정된 공간 크기를 가진 텐서를 출력합니다.
- AdaptiveAvgPool2d(1)은 각 공간적 영역 내의 값들을 평균하여 각 채널의 공간적 정보를 요약하며, 실질적으로 전역 평균 풀링 연산을 수행합니다.
- 분류 작업에서는 입력 특성 맵을 전역 컨텍스트나 공간적 불변성을 캡처하기 위해 AdaptiveAvgPool2d(1)로 처리한 후, 완전 연결 계층으로 전달하기 위해 주로 사용됩니다.
- Flatten():
- 주로 AdaptiveAvgPool2d(1) 연산 이후나 합성곱이나 풀링 계층 이후에 적용됩니다.
- Flatten()은 이전 계층의 출력 텐서를 입력으로 받아 해당 차원을 따라 모든 요소를 연결하여 1차원 텐서로 변환합니다.
- Flatten()의 목적은 공간적으로 구성된 특성 맵을 1차원 특성 벡터로 변환하여 완전 연결 계층이나 다른 1차원 입력을 기대하는 계층에 제공하기 위한 것입니다.
데이터셋 학습과정

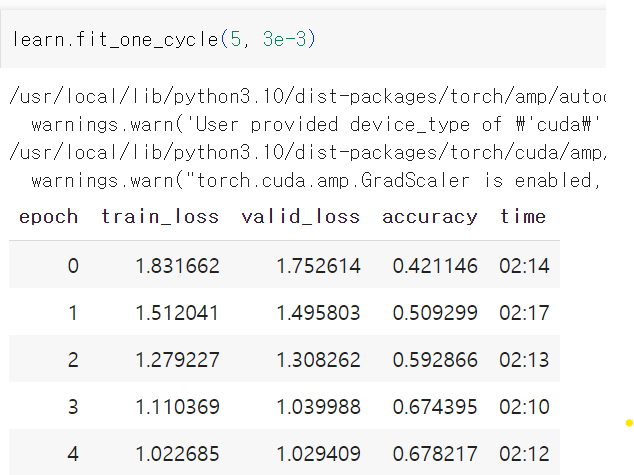
10개 범주 중 올바른 하나만을 선택해야 한다는 점을 고려하면 시작이 꽤 좋음. 더 깊은 모델을 사용한다고 해서(단순히 계층을 더 쌓아올린다고 해서) 성능이 무조건 좋아지는 것은 아님 => 스킵 연결이라는 개념 도입!!
♣ 14.2 현대적 CNN의 구축: ResNet
- Gradient Vanishing(Exploding)
CNN에서 파라미터를 업데이트할 때 기울기(Gradient) 값이 너무 작거나 크면 학습이 제대로 이루어지지 않을 수 있고, 학습 속도가 매우 느려질 수 있음. 여러 개선 방법이 고안되었지만 신경망의 깊이가 일정 수준 이상 깊어지면 여전히 기울기 값에 대한 문제가 발생함.
- 14.2.1 스킵 연결(shortcup connection)
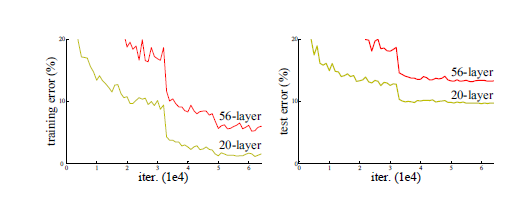
배치정규화를 사용했음에도 불구하고 더 많은 계층으로 구성된 신경망이 더 적은 계층의 신경망보다 성능이 뛰어나지 않은 문제 발생. 이러한 성능 저하는 과적합 때문이 아님. 또한 적당히 깊은 모델에 계층을 더 많이 추가하면 학습용 데이터셋에서 오차가 더 커짐. 깊은 레이어까지 잘 학습이 되도록 하는 방법 고민
해결방법1. 깊은 모델을 구성할 때 추가된 계층을 항등 매핑(identity mapping)으로 만들고, 그 외의 계층은 얕은 모델에서 학습한 내용을 그대로 복사하는 방식으로 문제 해결
예시) 잘 학습된 20개 계층의 신경망으로 시작해서, 아무 일도 하지 않은 36개 계층을 추가한다고 가정. 그 결과 56개 계층으로 구성했지만 20개 계층의 신경망과 정확히 같은 일을 하는 신경망이 만들어짐.
해결방법2. 모든 conv(x)를 x + conv(x)로 바꾸고 최종 배치 정규화 계층마다 gamma를 0으로 초기화하기. 그러면 추가 36개 계층에서 conv(x)는 항상 0이 됨. 즉 x + conv(x)는 항상 x와 같음. 추가 36개 계층이 항등 매피이지만 파라미터가 존재하기 때문에 학습이 가능함. 잘 작동하는 20개 계층의 모델로 시작해서 초기에는 아무 일도 하지 않는 추가 36개 계층을 더한 뒤, 전체 56개 계층의 모델을 미세 조정함. 그러면 추가한 36개 계층이 유용한 파라미터를 학습할 수 있음.
=> 레이어 간의 연결이 순서대로 연속적인 것만 있는 게 아니라 중간을 뛰어넘어 input을 전달하는 shortcut 추가.

기존의 신경망은 i번째 층과 (i+1)번째 층의 연결로 구성되어 있지만, ResNet은 i번째 층과 (i+r)층의 연결로 구성되어 있음. 그림을 보면 알 수 있듯이, Residual Learning에서는 정보 전달이 한 층을 건너 뜀. 즉, 지름길을 사용한다고 이해할 수 있는데, 이러한 연결 방식을 Shortcut Connection이라고 함. 이 방식을 사용하면 떨어진 두 개의 층을 연결함으로써 오차 역전파 시 기울기가 쉽게 전파된다는 장점이 있음.
기존 방식은 이웃한 층과의 연결만 있고, 입력값(x)를 받아 H(x)를 출력함. CNN은 학습 과정에서 가중치를 변경해가며 최적의 값을 찾아냅니다. 이를 통해 최적의 H(x)를 찾는 것을 목표로합니다. Residual Learning은 여기서 조금 다른 방식을 사용합니다. 위 그림 중 오른쪽과 같이 목표치를 H(x)가 아닌 F(x)+x로 세웁니다. 그 방식은 아래와 같습니다.
- 출력 결과는 H(x)가 아닌, H(x)와 입력값(x)의 차이로 설정함. 즉 목표는 H(x)-x. 이를 F(x)라고 가정. 즉 F(x)는 잔차
- 따라서 H(x) = F(x) + x. 원래 mapping은 F(x) + x로 재구성됨.
이 방식은 지름길을 통해 i층의 입력값 x를 (i+r)층의 출력값 F(x)에 더하는 연산만 추가되기 때문에 파라미터가 따로 필요 없음.
- 이 과정을 Identity Mapping이라고 정의함.
ResNet은 먼저 더 적은 계층으로 구성된 모델을 학습시킨 다음 마지막에 새로운 계층을 추가하여 미세 조정하는 방식을 사용하지 않음. 'CNN VS ResNet' 이미지에서 보는 것처럼 CNN 전체에서 ResNet 블록을 사용하고, 일반적인 방식으로 초기화와 SGD 학습을 해나감.
<영상 정리>

- x가 들어와서 F(x)가 나가는 게 기존, x가 들어와서 x+F(x)가 나가게끔 연결해 주는 게 skip-connection
- layer에 들어온 x를 받아서 만들고 싶은 이상적인 값이 H(x)일 때
- 이상적인 값을 F(x)로 만들기 VS x+F(x)로 만들기
- 후자가 학습이 훨씬 잘 됨
- H(x)가 x랑 비슷한 값이라고 가정했을 때 x가 H(x)가 되기 위해서는 기존의 모델이라면 conv(x)가 identity가 되어야 함(즉 항등 매핑이어야 H(x)가 될 것)
- ResNet 모델이라면 x+F(x)를 H(x)로 만들어야 하는데 H(x)가 x랑 비슷한 값이라고 했으니 conv(x)가 0이 되어야 함.
- identity를 만드는 것보다 0 matrix를 만드는 게 훨씬 쉽겠지
- 즉 skip-connetciont이 있을 때는 x랑 비숫한 H(x)를 만들기가 굉장히 쉬움. skip-connection을 연결한다는 것은 값의 변화가 그리 크지 않을테니 layer 하나에서 모든 걸 다 하려고 하지 말고 조금씩만 바꿔나가라는 신호를 주는 셈임.
- x와 x+F(x) 사이의 차이만 학습한다고 해서 '잔차 학습'이라고 함
항등 매핑
전혀 변형되지 않은 입력을 그대로 반환함. 항등 함수(identity function)가 이를 수행함.
ResNet의 장점
- 최적화가 비교적 쉬움
- 단순히 shortcut을 통해 x를 식에 추가하기만 하면 되기 때문에 기존 네트워크의 구조를 크게 변경하지 않고 학습을 진행시킬 수 있음
- 파라미터 수나 연산량의 증가도 없으며, 복잡도가 증가하지도 않음
- 깊은 신경망을 구성하더라도 vanishing 문제가 발생하지 않음. 전체 신경망에 걸쳐 가중치들을 최적화하는 것이 아니라 2-3개의 짧은 레이어들로 이루어진 Residual Block 마다 부분적인 학습이 진행되기 때문.
간단한 ResNet 블록 정의

- ResBlock(Module): 이 부분은 Module 클래스를 상속하여 Residual 블록을 정의합니다. Module은 PyTorch의 모듈 기반 클래스로, 사용자 정의 모듈을 만들 때 상속하는 기본 클래스입니다.
- __init__(self, ni, nf): 클래스의 생성자(constructor)입니다. ni와 nf는 두 개의 매개변수로 받습니다. 이는 Residual 블록의 입력 채널 수와 출력 채널 수를 지정하는 값입니다.
- self.convs = nn.Sequential(...) nn.Sequential(...)은 레이어들을 순차적으로 실행하는 PyTorch의 빌트인 클래스입니다. Residual 블록 내에서 컨볼루션 레이어 두 개를 순차적으로 실행하도록 구성합니다.
- ConvLayer(ni, nf) ConvLayer는 사용자 정의 함수로, 컨볼루션(Convolution) 레이어를 생성하는 역할을 합니다. 이 함수는 입력 채널 수 ni와 출력 채널 수 nf를 받아서 컨볼루션 레이어를 생성합니다.
- ConvLayer(nf, nf, norm_type=NormType.BatchZero) 위에서 정의한 ConvLayer와 비슷하지만, 이번에는 입력 채널 수와 출력 채널 수가 모두 nf로 동일합니다. 또한, norm_type=NormType.BatchZero 인자를 전달하여 Batch normalization을 사용하면서 마지막 배치 정규화 계층의 가중치를 0으로 초기화하는 방법을 적용합니다.
- def forward(self, x): return x + self.convs(x) forward 메서드는 PyTorch에서 모델을 통과할 때 호출되는 함수로, Residual 블록의 forward pass를 정의합니다. 입력 데이터 x를 받아서 self.convs(x)를 통과시킨 결과를 원래 입력 x와 더하여 반환합니다. 즉 x + F(x)를 반환하는 것. 이것이 Residual 블록의 핵심 아이디어인 "shortcut connection" 또는 "skip connection"으로, 네트워크가 깊어질 때 그레이디언트 소실 문제를 줄여주는 역할을 합니다. 결과적으로 네트워크가 더 깊어져도 더 잘 학습할 수 있게 됩니다.
두 가지 문제점
- 1 이외의 스트라이드를 처리할 수 없음
예를 들어 합성곱 중 하나가 스트라이드 2로 설정된다면 출력 활성의 격자 입력의 각 축의 크기가 절반씩 축소됨. 따라서 x와 출력 활성의 크기가 달라지므로 더할 수 없음. 입력과 출력의 연결 모양이 서로 다른 ni!=nf에서도 같은 문제 발생\
- ni=nf가 되어야만 함
* 내일 공부할 내용
nn.AdaptiveAvgPool2d(1) VS Flatten()
Gradient Vanishing & Exploding
※ 참고 자료
1. ResNet: https://m.blog.naver.com/siniphia/221382881525
CNN 모델 탐구 (6) - ResNet
1. 개요 CNN은 원론적으로 그 망이 깊어질수록 정확도가 향상된다는 것이 일반적인 견해이지만, G...
blog.naver.com
2. ResNet: https://www.youtube.com/watch?v=Fypk0ec32BU
'ResNet' 카테고리의 다른 글
| ResNet 만들기(stem, body, header) (0) | 2023.09.18 |
|---|---|
| Human Protein Atlas Image Classification(ResNet34) (0) | 2023.09.11 |
| (예시)ResNet 50 구현 (0) | 2023.07.23 |
| (논문)Deep Residual Learning for Image Recognition (0) | 2023.07.23 |
| (예시)Fruit Prediction|CNN|Pytorch|ResNet-18 (0) | 2023.07.17 |