2024. 2. 25. 12:42ㆍ딥러닝 모델: 파이토치
두 개의 선택지 중에서 정답을 고르는 문제를 이진 분류(Binary Classification)이라고 한다. 그리고 이진 분류를 풀기 위한 대표적인 알고리즘으로 로지스틱 회귀가 있다. 로지스틱 회귀의 알고리즘 이름은 회귀이지만 실제로는 분류 작업에 사용할 수 있다.
♣ 이진 분류(Binary Classification)
시험 성적에 따라 합격, 불합격이 기재된 데이터가 있다고 가정한다. 성적이 x라면 합격/불합격 결과는 y이다.

위의 데이터에서 합격을 1, 불합격을 0이라고 할 때 그래프를 그리면 아래와 같다.

이 그래프는 알파벳의 S자 형태로 표현된다. 이러한 x와 y의 관계를 표현하기 위해서는 Wx+b와 같은 직선 함수가 아니라 S자 형태로 표현할 수 있는 함수가 필요하다. 이런 문제에 직선을 사용할 경우 분류 작업이 잘 작동하지 않기 때문이다.
그래서 로지스틱 회귀의 가설은 선형 회귀 때의 H(x) = Wx+b 가 아니라 S자 모양 그래프를 만들 수 있는 특정 함수 f를 추가적으로 사용하여 H(x) = f(Wx+b)의 가설을 사용한다. 그리고 S자 모양 그래프를 그릴 수 있는 어떤 함수 f는 이미 널리 알려져 있다. 바로 시그모이드 함수이다.
♣ 시그모이드 함수(Sigmoid function)
참고: https://jy-deeplearning.tistory.com/29
시그모이드 함수의 방정식은 아래와 같다.
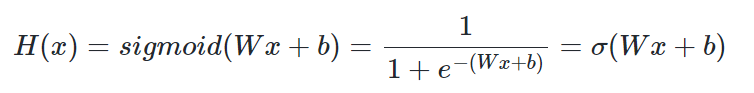
선형회귀에서 최적의 W와 b를 찾는 것이 목표였던 것처럼, 로지스틱회귀에서도 W와 b를 찾는 것이 목표이다.
W와 b가 함수의 그래프에 어떤 영향을 주는지 직접 그래프를 그려서 알아보자.
numpy를 이용하여 시그모이드 함수를 정의한다.

1. W가 1이고 b가 0인 그래프
w가 1이고 b가 0인 그래프를 그려보자.

위 그래프를 통해 시그모이드 함수가 출력값을 0과 1 사이의 값으로 조정하여 반환함을 알 수 있다. x가 0일 때 0.5의 값을 가지며, x가 매우 커지면 1에 수렴한다. 반면 x가 매우 작아지면 0에 수렴한다.
* plt.plot([0, 0], [1.0, 0.0], ':')에서 [0, 0]은 x축 좌표를 나타낸다. [1.0, 0.0]은 y축 좌표를 나타낸다. 즉 x가 0인 위치에서 y값이 1.0에서 시작하여 0.0에 이르기까지 내려가는 선을 그리는 것이다. 그런데 ':' 가 주어졌으므로 선이 점선으로 그려진다.
2. W값의 변화에 따른 경사도의 변화
이제 W값을 변화시키며 이에 따른 그래프를 확인해보자
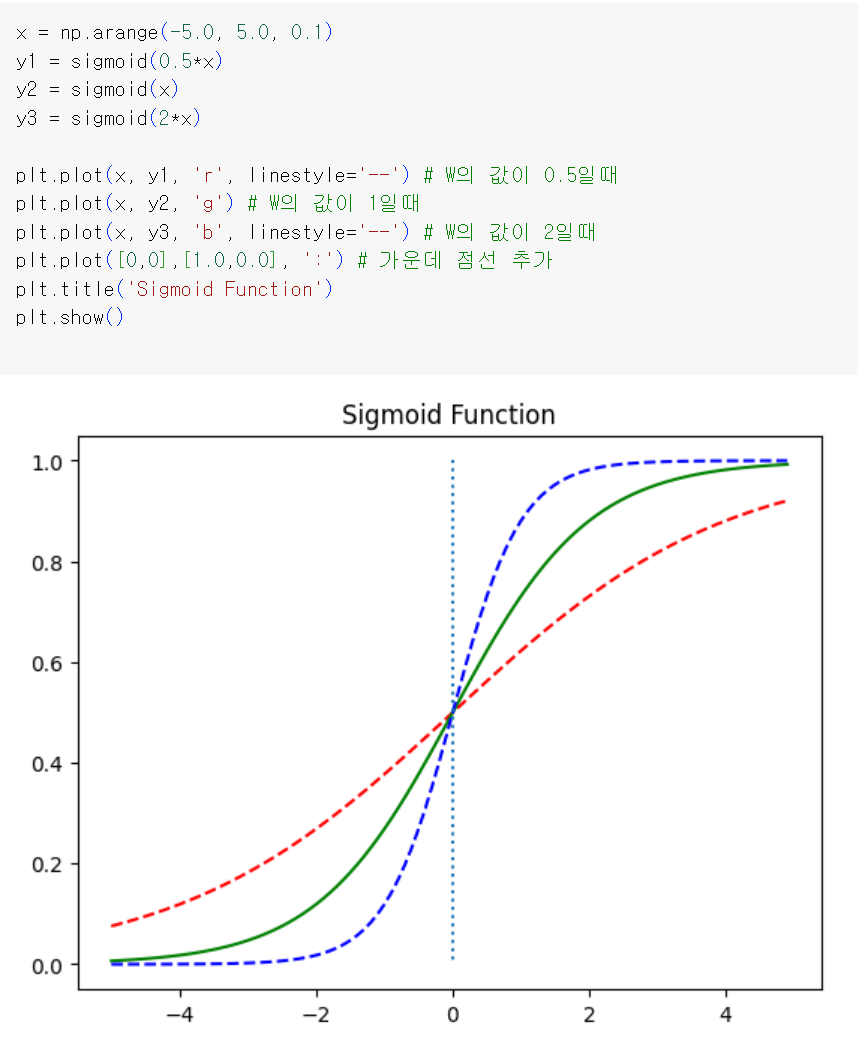
그래프를 보면 W 값에 따라 그래프의 경사도가 변하는 것을 볼 수 있다. 앞서 선형회귀에서 가중치 W는 직선의 기울기를 의미했지만 여기서는 그래프의 경사도를 결정한다. W값이 커지면 경사가 커지고 W값이 작아지면 경사가 작아진다.
3. b값의 변화에 따른 좌, 우 이동
b값에 따라 그래프가 어떻게 변하는지 확인해보자.

b의 값에 따라서 그래프가 좌, 우로 이동하는 것을 알 수 있다.
4. 시그모이드 함수를 이용한 분류
시그모이드 함수는 입력값이 한없이 커지면 1에 수렴하고, 입력값이 한없이 작아지면 0에 수렴한다. 시그모이드 함수의 출력값은 0과 1 사이의 값을 가지기 때문에 이 특성을 이용하면 분류 작업에 사용할 수 있다.
예를 들어 임계값을 0.5라고 정하면 출력값이 0.5 이상이면 1(True), 출력값이 0.5이하면 0(False)로 판단하도록 할 수 있다. 이를 확률이라고 생각하면 해당 레이블에 속할 확률이 50%가 넘으면 해당 레이블로 판단하고, 해당 레이블에 속할 확률이 50%보다 낮으면 아니라고 판단한다.
♣ 비용 함수(Cost function)
로지스틱 회귀의 가설이 H(x) = sigmoid(Wx+b) 인 것을 알았으니, 이제 최적의 W와 b를 찾을 수 있는 비용함수를 정의해야 한다. 앞서 선형회귀에서 배운 비용 함수인 평균제곱오차(MSE)를 로지스틱회귀의 비용함수로 사용할 수 있을까?
다음은 평균제곱오차의 수식이다.
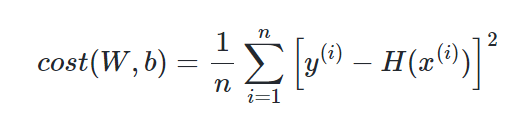
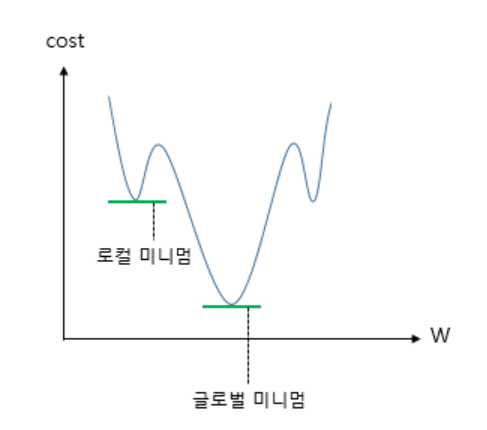
위의 비용함수 수식에서 H(x)를 Wx+b가 아닌 sigmoid(W(x) +b)로 바꾼 뒤 미분하면 선형회귀 때와는 달리 아래 그림과 유사한 비볼록(non-convex) 형태의 그래프가 나온다.
참고: https://jy-deeplearning.tistory.com/6
옵티마이저(최적화)의 의미와 경사하강법(Gradient Descent)
♣ 최적화(옵티마이저) 손실함수 값을 최소화하는 파라미터를 구하는 과정 즉 모델이 예측한 값과 실제값의 차이를 최소화하는 신경망 구조의 파라미터를 찾는 과정 손실함수 값의 변화에 따라
jy-deeplearning.tistory.com
위와 같은 그래프에서 경사하강법을 사용할 경우, 경사하강법이 오차가 최솟값이 되는 구간에 도착했다고 판단한 그 구간이 실제로 오차가 완전히 최솟값이 되는 구간이 아닐 수 있다. 최소가 되는 구간을 잘못 판단하면 최적의 가중치 W가 아닌 다른 값을 택하기 때문에 모델의 성능이 더 오르지 않는다. 따라서 평균제곱오차를 비용함수로 사용하는 것은 적절하지 않다.
시그모이드 함수의 특징은 함수의 출력값이 0과 1 사이의 값이라는 점이다. 즉, 실제값이 1일 때 예측값이 0에 가까워지면 오차가 커져야 하며, 실제값이 0일 때 예츠값이 1에 가까워지면 오차가 커져야 한다. 이를 충족하는 함수가 바로 로그 함수이다. 다음은 y=0.5에 대칭하는 두 개의 로그 함수 그래프이다.
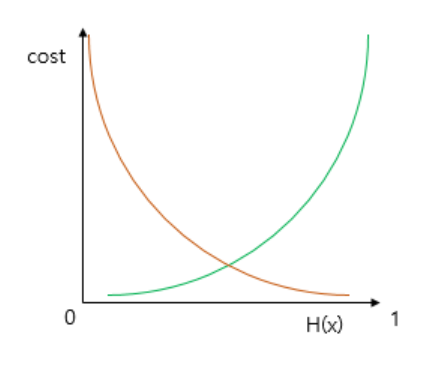
실제값이 1일 때의 그래프를 주황색 선으로 표현하였으며, 실제값이 0일 때의 그래프를 초록색 선으로 표현하였다.
실제값이 1이라고 할 때, 예측값인 H(x)의 값이 1이면 오차가 0이므로 당연히 cost는 0이 된다. 반면 H(x)가 0으로 수렴하면 cost는 무한대로 발산한다. 실제값이 0인 경우는 반대이다.
두 개의 로그 함수를 식으로 표현하면 다음과 같다.

이는 하나의 식으로 통합할 수 있다.

실제값 y가 1이면 덧셈 기호를 기준으로 우측의 항이 없어지고, 실제값 y가 0이면 덧셈 기호를 기준으로 좌측의 항이 없어지기 때문에 식을 하나로 합칠 수 있다.
선형회귀에서는 모든 오차의 평균을 구해 평균 제곱 오차를 사용했었다. 여기서도 모든 오차의 평균을 구한다.
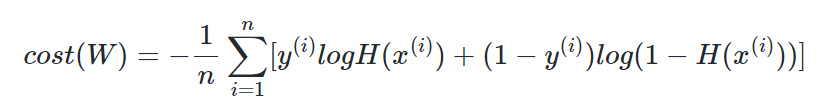
위 비용함수를 이용하여 경사하강법을 수행하면 최적의 가중치를 찾을 수 있다.
'딥러닝 모델: 파이토치' 카테고리의 다른 글
| Pytorch로 시작하는 딥러닝 입문(04-03. nn.Module 로지스틱 회귀 구현하기) (0) | 2024.02.27 |
|---|---|
| Pytorch로 시작하는 딥러닝 입문(04-02. 파이토치로 로지스틱 회귀 구현하기) (0) | 2024.02.25 |
| Pytorch로 시작하는 딥러닝 입문(03-08. 벡터와 행렬 연산 복습하기) (0) | 2024.02.24 |
| Pytorch로 시작하는 딥러닝 입문(03-07. 커스텀 데이터셋, transform 약간, ToTensor) (0) | 2024.02.24 |
| Pytorch로 시작하는 딥러닝 입문(03-06. 미니배치와 데이터로드) (0) | 2024.02.21 |